One of the topics in physics that drove me almost crazy 48 years ago was a paradox related to the relativistic length contraction effect. This effect is an elementary consequence of Einstein’s Special Theory of Relativity [STR]. Paradoxes in this context are almost always based on two separate, but seemingly consistent descriptions of a series of kinematic events in two inertial frames. These descriptions seem to lead to contradicting results.

One such paradox is the “rod/slot paradox” – a variant of the Rindler-Shaw paradox. Let us call it RS-paradox below. It says that in one inertial frame a falling rod will move through a slot in a plate (or in the ground) – and in another frame it would not. In both (!) cases due to the length contraction effect. (I will present a related scenario in more detail below.)

Physics students get trained to achieve consistent descriptions of natural events independent of their choice of a “frame of reference” (a defined coordinate system) – and in particular independent of a choice between coordinate systems of so called “inertial systems” (which move with constant velocity vs. each other; see below). Inertial systems are fundamental in physics. The equivalence and the consistency of physical statements as well as measurements in inertial frames are mandatory for the correct formulation of the basic laws of physics. No wonder that unresolved paradoxes resulting from transitions between such reference frames may drive some students of physics crazy.

I got confronted with the RS-paradox for the first time when I was 17 and visited a physics course in a German Gymnasium. Special Relativity [SR] was a topic that occupied us for a few months. Our teacher presented us the RS-paradox with the help of a “ski-jumper” (see below) falling or not falling through a slot in the ground. My teacher admitted that he could not resolve the paradox for us – and as so many teachers (and introductory text books) he referred to a complicated theory of Rindler regarding modifications of stiffness and elasticity in the STR. This was, however, not very satisfactory for us students. Rightfully, we had the suspicion that a basic contradiction like the one given above should disappear already on a very basic level of argumentation.

The paradox gave me some sleepless nights in 1976, until I gave up at that time and trusted in some personal breakthrough in the future. Later, at university and during my PHD, I just applied SR-formulas whenever necessary. No time for deeper explanations of paradoxes. However, some years ago – long after my professional time in physics – the problem entered my mind again. I used some relaxed time in Norway to work a bit with it once again. And this time I could resolve it in a personally satisfactory way. As the basic points of the solution are in the end rather simple, I would like to present them here in a post series – and maybe save some physics students a few sleepless night.

So, this is a post series for folks interested in physics and math.

Hint: This post has been changed and rewritten on 10/24/2024 and 12/06/24. Sorry for any inconvenience.

Requirements

Requirements regarding math are:

• You should be familiar with the idea of a 2- or 3-dimensional Cartesian coordinate system. Although it would in principle be possible to use coordinates systems with curvilinear coordinates (as e.g. spherical coordinates) we will refrain from doing so for the sake of mathematical simplicity.
• You should have an elementary idea of position and velocity vectors defined in an Cartesian coordinate system and what their components mean.
• Our topic requires various changes of the point of view and between multiple Cartesian coordinate systems attached to different objects in motion. This may require rotations of the Cartesian coordinate systems – or equivalently projections of position and velocity vectors onto differently oriented axes. We will derive respective data by elementary rules of geometry.
• You should not be afraid of formulas, some geometry and elementary trigonometric relations.

Requirements regarding physics are the following:

• You should have learned about inertial frames and reference frames. For short definitions see below.
• You should be familiar with the Lorenz-transformation [LT] in STR in its elementary form. This covers the relation of coordinate measurements performed in two reference frames with their x-coordinate axes aligned along the line of their relative relative motion. The LT formulas then directly affect only the transformation of the x-coordinates and of the time coordinates of events between the inertial frames. y– and z-coordinates of events remain the same.
• You should be familiar with the effect that events observed to occur simultaneously in one inertial frame may be measured to occur at different points in time in another inertial frame.
• You should have understood the term “proper length” for the length of an object measured in a reference frame in which the object is at rest.
• You should also have learned about the length contraction effect – i.e. the effect that the length of a moving stick is measured to be shorter than the length measured in a frame where the stick is in rest – and the related premises. This includes the correct measurement procedure for the determination of the spatial distance between two events in an inertial system. To do this correctly the spatial coordinates of the events must be determined at the same point in time in the respective reference frame.
• You should know about the time dilation effect – and how it is derived from the LT formulas. You should be aware of its impact on the different velocity components of moving objects measured in different reference frames.

My main target group of readers are interested students attending a physics course in high school or in a German gymnasium. They are, in my opinion, fully equipped to resolve the rod/slot paradox without complex matrix and vector formalisms taught at university.

Inertial frames, reference frames and events

I shortly give a short definitions of some important terms.

• An “inertial frame” is one in which any object that experiences no force moves with zero or constant uniform velocity along some straight line.
• An inertial frame thus is one that moves with constant velocity (along a straight line) relative to another such frame or relative to some force-free objects under observation.
• We define a “reference frame” in our context as a coordinate system of an inertial frame. As said above we will use Cartesian systems to cover the spatial coordinates.
• We will often compare observations made in one inertial frame with those of an observer in another inertial frame. To do so we need to compare the spatial and time coordinates determined in each of the respective reference frames for distinct events. An event is (among other things) characterized by its spatial coordinates and its time coordinate.
• Each of the respective coordinate systems will have a defined orientation with respect to the constant uniform velocity of the reference frames’ movement versus one another.
• An observer in an inertial system reflects a dense coverage of the space by synchronized clocks in the sense that the observer has access to precise time data for all events measured at spatial positions in our coordinate systems. This is to a certain degree a theoretical idealization. The important point is the synchronization of all clocks in a reference frame ahead of any measurements.

Flat Euclidean geometry
We work in a standard Euclidean space of two or three dimensions: In such a “flat” space the standard laws of Euclidean geometry, which one learns in high school, apply. Space or space-time have no “curvature”. The spatial geometry in our inertial frames follows Euclidean laws globally. E.g. the law of Pythagoras holds everywhere and over long distances. In this respect STR is different from Einstein’s “General Theory of Relativity”. Just to remind us about this, I will use the abbreviation ECS for the (Cartesian) coordinate system of an inertial frame in our pure STR context.

Discussion of collision and collision-free scenarios

I will start this series with a simple naive presentation of the RS-paradox below. Later on, I will turn to a precise and detailed description of a “collision scenario“. I will set up a special thought experiment, in which a rod approaches a plate with a slot with a constant relative velocity along a diagonal line. The orientation of the rod and the slot will be aligned in a certain reference frame. Afterwards, I will define further main reference frames to cover the scenario from different perspectives.

For the collision scenario an observer in one of the frames clearly predicts a collision between the rod and the plate, while in the another frame one could naively expect the opposite, namely a transit of the rod through the slot. I will investigate some key events and apply the Lorentz transformation to describe the events in all reference frames.

We will see that the mathematics of the transformation equations will provide us with some valuable insights, which in the end help to grasp the cause of paradoxes. After having resolved the paradox for the “collision scenario” I will turn to a second collision-free “transit scenario” and present a detailed discussion for it – including three different observer perspectives. Eventually, we will come to the following conclusion:

If an observer in a selected reference frame predicts a collision or a transit, then also observers in other reference frames will predict a collision or a transit, respectively. The measurements performed by different observers will not contradict each other for either scenario. Instead we have to conclude that a collision scenario differs in its initial conditions fundamentally from a transit scenario – in all relevant reference frames.

What we will come to understand is that both scenarios should not and cannot be mixed – as it is (unfortunately) done in usual presentations of the RS-paradox. Actually, the paradox does not exist; it results from presenting two scenarios as fully equivalent, while they are not.

A typical naive presentation of the paradox

My teacher described the RS-paradox in the following way: He used a (somewhat nonphysical) ski-jumper with long skis who jumped from a height h down to the flat ground having a slot and a cave below it.

 

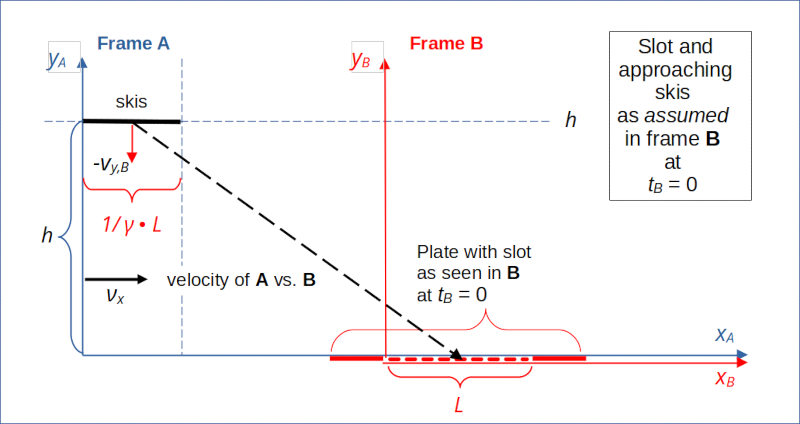
Illustration 1: Skis approaching a horizontally aligned slot in the ground.

He suggested a frame of reference B fixed at the ground. Frame B was equipped with a 2-dimensional spatial coordinate system with the x_B-coordinate axis stretching in parallel to the ground and a y_B-coordinate axis pointing vertically upwards. All clocks in the spatial grid of frame B were synchronized. Events were described via space and time coordinates [x_B, y_B, t_B].

The ski-jumper was assumed to move with two constant velocity components in frame B: v_j,x,B = const parallel to the ground and ν_j,y,B = ν_y,B = const in vertical direction down towards the ground, i.e. ν_j,y,B < 0 (ν_j,y,B = – v_y,B = const) . In contrast to a real ski-jump a constant velocity in y-direction is, of course, a simplification.

The jumper’s skis were always oriented in parallel to the ground, i.e. in x-direction. (By whatever means the ski-jumper managed to control this.) The skis had a proper length L_ski = L. I.e. this length was measured when the skis were at rest.

At the position where the ski-jumper would touch the ground ground a wide slot was assumed to exist (in the ground) with a proper length L in x-direction (measured in frame B). The slot had a fixed position in B. The velocities of the jumper were defied such that the middle of the skis touched ground in the middle of the slot (in x-direction). Below the slot some underground cave was located with big dimensions in all directions. Anyone falling through the slot would end up in this cave.

Because of the assumption v_j,x,B = ν_x = const., our teacher could introduce a second frame A co-moving with the ski-jumper in x-direction. Frame A had its own coordinate system with synchronized clocks everywhere. The orientation of the x- and y-axes in A were the same as in B. Observers in A registered events with coordinates [x_A, y_A, t_A]. A moved relative to B with velocity v_A,B = v_x. The x-axis of A overlaps with that of B. The ski-jumper thus moved in A with negative velocity v_j,y,A = -v_y,A = const. in y-direction. (v_y,A typically is not identical to ν_y,B due to the rules of velocity transformations in the STR).

At time t_A = t_B = 0 the ski-jumper was at a position x_B = 0 and y_B = h in B – having already reached his constant velocity components. (We safely ignore the problem of how we had accelerated the jumper to reach these velocities).

Description of the situation in reference frame B with the slot at rest
In our reference frame B the ski-jumper moves in diagonal direction towards the ground. Due to the length contraction effect the ski-length measured in B becomes shorter than their proper length L [L_ski,B < L], while the slot keeps up its proper length L [L_slot,B = L]. Therefore, we might think that the ski-jumper will fall into the cave. It, at least, sounds logical …

 

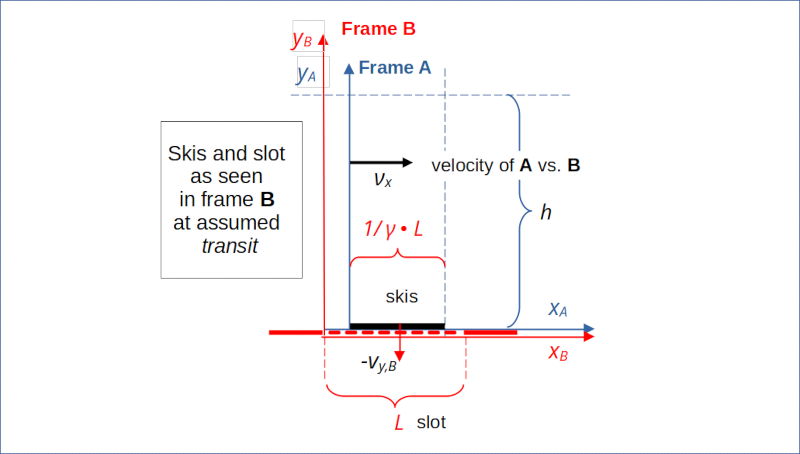
Illustration 2: Assumed transition of the rod as seen from frame B

Description in a reference frame A co-moving with the the ski-jumper in x-direction
Now let us look at a seemingly natural description of the same scenario by an observer in frame A.

 

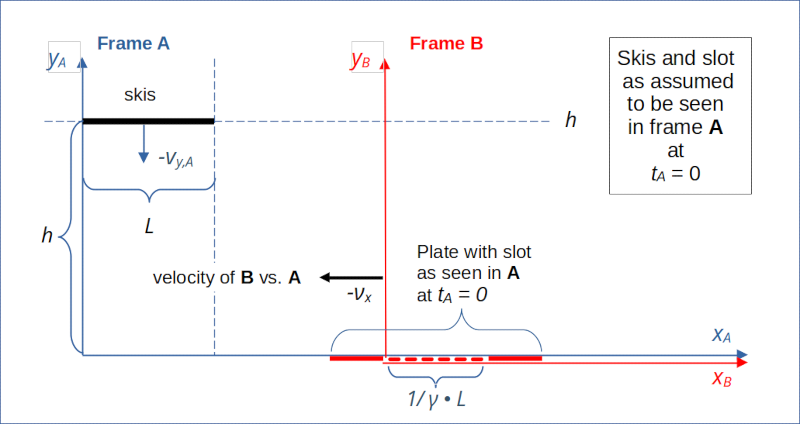
Illustration 3: Assumed description of the scenario from the perspective of frame A

This observer would find a horizontal velocity of the jumper ν_j,x,A = 0. We ignore the question about the value of the constant vertical ν_y,A for the time being. In frame A the skis are in rest regarding their horizontal movement. Therefore, their length is L_ski,A = L. However, due to length contraction the length of the slot moving with velocity v_slot,A = – ν_x relative to A is found to be shorter than L: L_slot,A < L. Therefore, we come to the conclusion that the ski-jumper will not fall into the cave, but instead experience a hard landing.

 

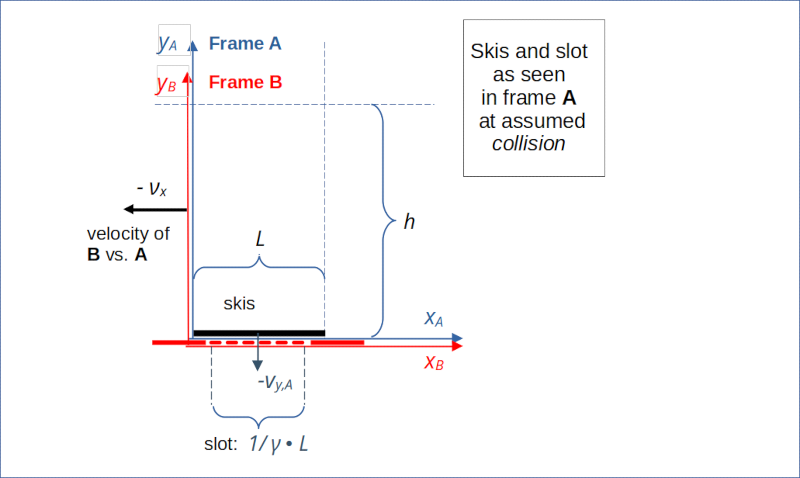
Illustration 4: Description of a collision from the perspective of frame A.

We have a paradox, as both descriptions appear to be right. Nevertheless, they obviously lead to a severe contradiction. One suspects a mistake in the assumptions. But what is actually wrong might be difficult to identify.

Other variants of the paradox exist in which no vertical movement happens, but gravity is assumed to work when a fast “ski-glider” moving horizontally passes the slots left end. In my opinion scenarios without gravity, but including a vertical or diagonal movement of the skis or a rod with a constant velocity, are much clearer. Therefore, I will stick to such scenarios.

Diagonal motion of objects and of attached reference frames

Some of the reference frames above display diagonally moving objects (with constant velocity components). What happens when we introduce reference frames attached to such diagonally moving objects? How can we apply the simple 1-dimensional form of the Lorentz Transformation to a given reference frame and another one that moves diagonally in the coordinate system of the first one?

Answer: We cannot apply it directly as the 1-dimensional form of the Lorentz Transformation does not refer to “diagonally” moving reference frames. For a coordinate independent representation of the LT relations we would need a full vector formalism. But, even without a such a formalism, there is, of course, a way out: We can shift the origins of our coordinate systems and rotate our coordinate axes such that the x-axes align with the measured line of relative motion. Afterwards, we may again apply the familiar simple form of the Lorentz Transformation.

So, it is foreseeable that we will sometimes be forced to shift and rotate our coordinate systems. This inevitably will bring trigonometric operations with it. And, beyond trigonometry, there is a major pitfall: Observers in different inertial frames with basically the same orientation of their coordinate axes may measure different angles between their x-axes and the line of their relative (diagonal) motion vs. each other. This may come as a surprise to you – and this interesting point will indeed require some major effort and careful analysis in this post series.

The good news is that math on the level taught at high school or in a German gymnasium is sufficient to cover all of the transformations completely.

How do we proceed from here?

My line of work will be the following: Instead of applying the length contraction directly, I will focus on some events defined by a scenario and its initial conditions. I will then apply the Lorentz Transformation to transform the events’ coordinates between my chosen frames of reference. By doing so, we will get a lot of important insights.

But a first step is a more precise definition of a scenario and its initial conditions. In the next post I will turn to the setup of a collision scenario inspired by the last two illustrations above.

Special relativity and the rod/slot paradox – II – setup of a collision scenario

In further forthcoming posts we will learn that the Lorentz transformation implies a rotation of some objects in question. Stay tuned ….