Special relativity and the rod/slot paradox – XVI – perception of rod/slot collision in a diagonally moving frame

We continue with our analysis of the 2-dimensional rod/slot paradox in Special Relativity. We consider the perception of observers in a reference frame W. This special frame moves diagonally with respect to a setup frame A, which we used to define a collision scenario between rod and slot (see the first posts in this series). The Lorentz Transformation [LT] told us the following: In comparison to A, the rod and slot have differently rotated orientations in W versus the line of relative motion between A and W. The rod is in addition rotated versus the LT’s image of A‘s x-axis of A. We also found peculiar orientations of the respective velocity vectors in W.

In this post we will show that the perceived data for the collision scenario (!) predict an inevitable collision of both objects in W, too. This is fully consistent with the results we previously got for observers in other reference frames – in particular for observers moving with the colliding objects.

Just to be clear: A profoundly different “transit scenario” (see the 8th to the 12th post of this series ) would, of course, be perceived differently and allow the rod to pass through the slot without collision. Also in W.

Initial conditions – frames A and W – and the collision scenario

The initial conditions both for the collision scenario and for the diagonal movement of frame W versus frame A are depicted in the next drawing. The reader who has followed this post series is familiar with it, already.

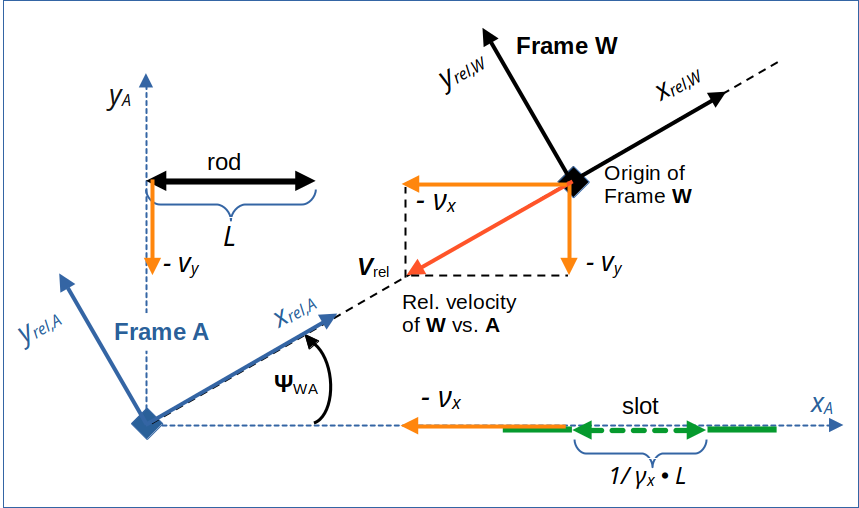
Initial conditions and rotated coordinate systems of frames A and W

Illustration 1: A diagonally approaching frame W in our collision scenario, which was set up in a frame A (see the first 3 posts of this series). Rod and slot meet each other at t_A = t_W = 0. For the Lorentz Transformation from A to W we use rotated Cartesian coordinate systems with x-axes oriented along the line of relative motion of the frames vs. each other.

For notations, quantity names and abbreviations see the preceding posts. v_rel is the vector of relative velocity of the origins of our two frames versus each other.

Conditions of the collision scenario as perceived by an observer at rest in frame W

The calculations performed in the preceding posts have revealed the following situation in W at t_W = 0:

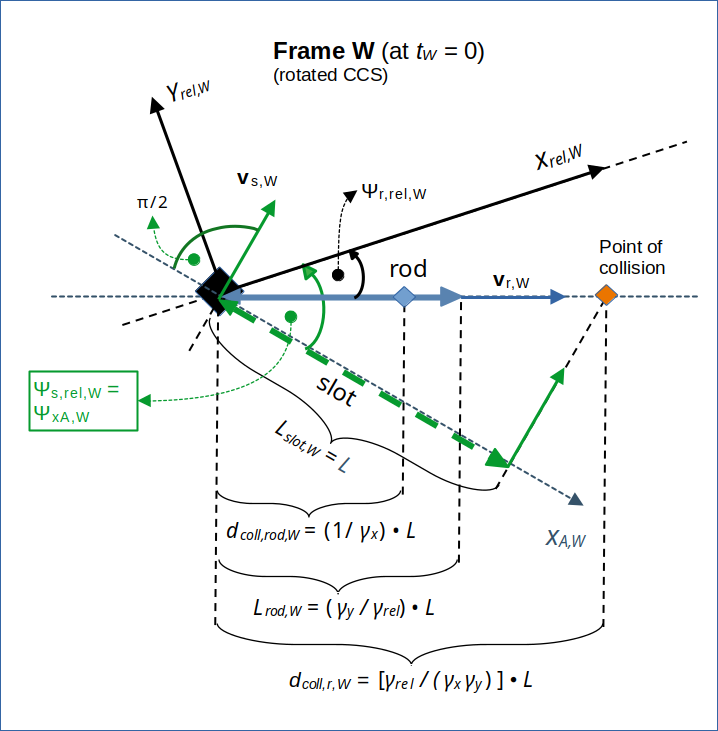
Collision scenario, position and velocity vectors in diagonally moving frame W

Illustration 2: A diagonally approaching frame W in our collision scenario, which was set up in a frame A. For the Lorentz Transformation from A to W we use rotated Cartesian coordinate systems with x-axes oriented along the line of relative motion of the frames.

v_s,W and v_r,W are the velocity vectors of our two objects, namely the slot and the rod, respectively. v_s,W is perpendicular to the slot. v_r,W is aligned with the rod’s orientation. See the preceding post for a proof.

The attentive reader recognizes some distances in illustration 2 for which we yet have to provide a mathematical derivation. Furthermore we have to strictly prove that a collision is observed in W at all.

In case we succeed, we would once again have shown that the so called “Thomas-Wigner rotation” in the Theory of Special Relativity helps to ensure consistency in the descriptions of multi-dimensional object movements and related events by observers attached to different reference frames.

Derivation of the location of the (potential) collision point between rod and slot in W

Let us first derive where (from the perspective of an observer in W) the point of collision is located in W. Illustration 2 above gives us a guideline.

The velocity of the slot is vertical to the slot’s orientation and points upwards. The velocity vector of the rod is instead aligned with the rod’s orientation. We further know already (see the 14th post) that the angle between slot and rod fulfills the following conditions:

\[ \begin{align} \cos \left(\Psi_{s,r,W} \right) \,&=\, \gamma_x \, {\gamma_y \over \gamma_{rel}} \,, \\[8pt] \sin \left(\Psi_{s,r,W} \right) \, &=\, – \, \gamma_x \, \gamma_y \, \beta_x \, \beta_y \,. \end{align} \]

\[ \]

So, the slot hits the rod (potentially) at a point on a line aligned with the rod’s orientation and the rod’s path. This point has a distance d_coll,r,W from W‘s origin on the rod’s line of motion of

\[ \begin{align} d_{coll,r,W} \,&=\, {1 \over \cos\left(\Psi_{s,r,W} \right) } \, L \quad \Rightarrow \\[8pt] d_{coll,r,W} \, &= \, {\gamma_{rel} \over \gamma_x\, \gamma_y} \, L \,. \end{align} \]

This determines its spatial coordinates of the collision point relative to the origin of W (and with respect to a coordinate system of W with x-axis along the line of relative motion) completely.

Note that we, so far, must speak of a potential collision in W, because we have not yet proven that the rod moves fast enough to ensure that it hits the right end of the slot at the time of the potential collision.

Derivation of the collision time in W by geometrical reasoning

The absolute value of the slot’s velocity in W is (see the preceding post)

\[ v_{s,W} \,=\, \gamma_x\, \beta_y * c \,. \]

We can derive the time coordinate t_coll,W of the (potential) collision by dividing the vertical distance of the collision point from the slot by the slot’s velocity

\[ \begin{align} t_{coll,W} \,&=\, {1 \over \cos\left(\Psi_{s,r,W} \right) } \, L * \sin\left(|\Psi_{s,r,W}|\right) * {1 \over v_{s,W}} \\[8pt] &= \, {\gamma_{rel} \over \gamma_x\, \gamma_y} \, L * { \gamma_x \, \gamma_y\, \beta_x\,\beta_y \over \gamma_x \, \beta_y \, c} \,, \\[8pt] t_{coll,W} \,&=\, \beta_x \,{ \gamma_{rel} \over \gamma_x} \, {L \over c} \,. \end{align} \]

Derivation of the location of the (potential) collision point via Lorentz Transformation from frame A

An alternative way to get the location of the collision point is to transform the components of the collision point from A to W. Due to the setup conditions of the collision scenario In A we know that the collision occurs there at t_A = 0 and at a position with the following x-coordinate in the standard coordinate system

\[ x_{coll,A} \, = \, {1 \over \gamma_x}\, L\,, \quad y_{coll,A} = 0 \,. \]

The respective coordinates x_coll,rel,A and y_coll,rel,A in the rotated coordinate system (with x-axis aligned with the line that connects the origins of A and the approaching W) are derived from projections of the position vector. The cosine and the sine between the x-axis of A and the line of relative motion of W vs. A lead to the following components in the rotated coordinate system

\[ \begin{align} x_{coll,rel,A} \,&=\, {1 \over \gamma_x} \, {\beta_x \over\beta_{rel}} \, L \,, \\[8pt] y_{coll,rel,A} \,&=\, {1 \over \gamma_x} \, {\beta_y^2 \over \beta_{rel}} \, L \,. \end{align} \]

It is easy to show that the Lorentz Transformation to W has the result

\[ \begin{align} x_{coll,rel,W} \,&=\, {\gamma_{rel} \over \gamma_x} \, {\beta_x \over\beta_{rel}} \, L \,, \\[8pt] y_{coll,rel,W} \,&=\, {1 \over \gamma_x} \, {\beta_y^2 \over \beta_{rel}} \, L \,. \end{align} \]

From this we can calculate the length D_coll,W of the respective position vector to the collision point in W. After some steps and using the definitions of the relativistic factors we find

\[ \begin{align} D_{coll,W} \,&=\, {\gamma_{rel} \over \gamma_x\, \gamma_y} \, L \quad \Rightarrow \\[8pt] D_{coll,W} \,&=\, d_{coll,r,W} \,. \end{align}\]

In addition the angle Ψ_coll,rel,W of the position vector with the x_rel-axis of the rotated coordinate system in W is

\[ \begin{align} \cos \left( \Psi_{coll,rel,W} \right) \,&=\, {x_{coll,rel,W} \over D_{coll,W} } \,= \, \gamma_y \, {\beta_x \over \beta_{rel}} \quad \Rightarrow \\[8pt] \cos \left( \Psi_{coll,rel,W} \right) \,&=\, \cos \left( \Psi_{r,rel,W} \right) \,. \end{align}\]

This means that the collision point indeed is located on the path of the rod in W. And the results of the present calculation are, of course, identical to the results of the previous first derivation above.

Derivation of time to collision via Lorentz Transformation from A

The LT from A to W delivers the collision time in W as

\[ \begin{align} t_{coll,W,LT} \,&=\, \gamma_{rel} * \left( 0 \,+\, { v_{rel} \over c^2 } \, x_{coll,rel,A} \right) \\[8pt] \,&=\, {\gamma_{rel} \over \gamma_x } \, \beta_x \,{L\over c^2} \quad \Rightarrow \\[8pt] t_{coll,W,LT} \,&=\, t_{coll,W} \,. \end{align} \]

Has the right end of the rod moved beyond the assumed point of collision at collision time?

A necessary condition for a collision is: The right end of the rod must have moved beyond the point of collision. This is indeed the case. According to preceding posts the rod has a length L_rod,W and a velocity value v_rod,W given by

\[ L_{rod,W} \,=\, {\gamma_y \over \gamma_{rel} } \, L\,, \quad v_{r,W} \,= \, \gamma_y\,\beta_x \, c \,. \]

Thus the right end of the rod moves to a position along the rod’s path with a distance d_r,r,coll,W to the origin given by

\[ \begin{align} d_{r,r,coll,W} \,&=\, {\gamma_y \over \gamma_{rel} } \, L\, + \, v_{r,W} * t_{coll,W} \\[8pt] &=\, {\gamma_y \over \gamma_{rel} } \, L\, + \, \beta_x \, {\gamma_{rel} \over \gamma_x} \, {L\over c} * \gamma_y\,\beta_x \, c \\[8pt] &= \, {\gamma_{rel} \over \gamma_x \, \gamma_y} \,L \, \left( \, {\gamma_y^2 \, \gamma_x \over \gamma_{rel}^2 } \,+\, \gamma_y^2 \,\beta_x^2 \,\right) \,. \end{align} \]

This means that we have to ensure

\[ {1 \over \gamma_{rel}^2} \, \gamma_x \, \gamma_y^2 \,+\, \gamma_y^2 \, \beta_x^2 \,\gt\, 1 \,. \]

Let us reorder the expression on the left side:

\[ \begin{align} {1 \over \gamma_{rel}^2} \, \gamma_x \, \gamma_y^2 \,+\, \gamma_y^2 \, \beta_x^2 \,&=\, \gamma_y^2 \,\left( \,\gamma_x\,( 1 \,-\, \beta_x^2 \,-\, \beta_y^2 ) \,+\, \beta_x^2 \, \right) \\[8pt] &= \, \gamma_y^2 \,\left( \, \gamma_x \,(1 \,-\,\beta_y^2)\, -\, \beta_x^2\,(\gamma_x \,-\, 1) \, \right) \\[8pt] &= \, \gamma_x \, – \, \gamma_y^2\, \beta_x^2 \, (\gamma_x \,-\, 1) \\[8pt] &= \, \gamma_x \, ( 1 \,-\, \gamma_y^2\,\beta_x^2) \,+\, \gamma_y^2\, \beta_x^2 \end{align}\]

This means

\[ \begin{align} &\gamma_x \, ( 1 \,-\, \gamma_y^2\,\beta_x^2) \,\gt\, 1 \,-\, \gamma_y^2\, \beta_x^2 \quad \Rightarrow \\[8pt] &1 \,-\, \gamma_y^2\, \beta_x^2 \,\gt\, 0 \quad \Rightarrow \\[8pt] &1 \,-\, {1 \over 1 \,-\, \beta_y^2} \, \beta_x^2 \,\gt\, 0 \quad \Rightarrow \\[8pt] &\gamma_y^2 \,\left( \, 1 \,-\, \beta_y^2 \,-\, \beta_x^2 \,\right) \,\gt\, 0 \quad \Rightarrow \\[8pt] &\gamma_y^2 \, {1 \over \gamma_{rel}^2 } \,\gt\, 0 \,. \\[8pt] \end{align}\]

The last statement is obviously true, because γ_rel is bigger than γ_y. This is however not sufficient for the perception of a real collision in W.

Point on the rod where the collision occurs

A sufficient condition would be that the assumed point of the collision on the rod’s path is a point on the rod to the right of the rod’s left end. To prove this we calculate the position d_coll,rod,W (t_W=0) of the collision point on the rod at the point t_W = 0 in time. We just have to apply the velocity of the rod to this particular point on the rod and go backwards in time:

\[ \begin{align} &d_{coll,rod,W} (t_W= 0) \,\\[8pt] &=\, d_{coll,r,W} (t_W= t_{coll,W} ) \,-\, v_{r,W} * t_{coll,W} \\[8pt] &= \, {\gamma_{rel} \over \gamma_x\, \gamma_y} \, L \,-\, \gamma_y \, \beta_x \, c * \beta_x \, {\gamma_{rel} \over \gamma_x} \, {1 \over c} \, L \\[8pt] &= \, {\gamma_{rel} \over \gamma_x\, \gamma_y} \, L \, \left[ \, 1\,-\, \gamma_y^2 \,\beta_x^2 \, \right] \\[8pt] &= \, {\gamma_{rel} \over \gamma_x\, \gamma_y} \, L \, \gamma_y^2 \, \left[ \, 1\,-\, \beta_x^2 \,-\, \beta_y^2 \, \right] \\[8pt] &= \, {1 \over \gamma_x} \, {\gamma_y \over \gamma_{rel}} \, L \\[8pt] &= \, {1 \over \gamma_x} \, L_{rod,W} \quad \lt \, L_{rod,W} \,. \end{align}\]

This confirms, by the way, results of previous posts.

Conclusion

In this post we have proven the following: An observer in a frame W, which diagonally approaches a setup frame A for the collision scenario, predicts a collision between the rod and the slot.

Once again we have shown that the collision scenario is consistently perceived by observers in very different frames of reference. The Lorentz Transformation and the Thomas-Wigner rotation of moving objects in two dimensions obviously guarantee a consistent description of a collision scenario. There are no contradictions and the proclaimed paradox has no real physical foundation.

Frame W is closely related to a frame Z, in which we have defined a “transit scenario”. This means that our two different scenarios, which we have analyzed in detail in this post series, must have substantially different initial conditions. From what we know so far the differences must be related to the initial angle between the rod and the slot. We turn to this point in the next post.

Stay tuned ….