Special relativity and the rod/slot paradox – X – details of the transit scenario as seen by the rod

In this post series we study the rod/slot “paradox”. During the last two posts we got familiar with a “transit scenario” prepared in a special reference frame Z, where the rod and the slot moved along the x– and the y-axis, respectively. We have again derived a comforting result: Both observers in the setup frame Z and a frame C co-moving with the rod measure and consistently describe a collision-free encounter of the rod and the slot: The slot moves through the slot.

This result was again due to a somewhat surprising effect of the Lorentz Transformation [LT] equations of Einstein’s “Special Theory of Relativity”. Analogously to the “collision scenario” we found a rotation of one of the objects (here of the slot) and a resulting inclination between the slot and the rod in the rod’s frame – although the rod was aligned with the orientation of the slot in the setup frame. Basic reasons were the non-simularity of events after the application of the LT and a subtle combination of time dilation and length contraction effects. This time the effects allowed for a transit of the rod through the slot. Or equivalently: The slot passes the rod diagonally with a proper timing to avoid any collision with the plate around the slot.

In this post we look at some details which an observer in the rod’s frame measures during the transit. This will prepare us for a further posts in which we will deal with direct transformations of events seen by an observer attached to the slot and an observer attached to the rod.

Angles and special points on the slot

Analogously to the collision scenario we can identify some special points and a related distance sequence along the x-axis in the frame of the object that moved horizontally in the setup frame. In the “transit scenario” (see the 8th post of this series) this object is the rod.

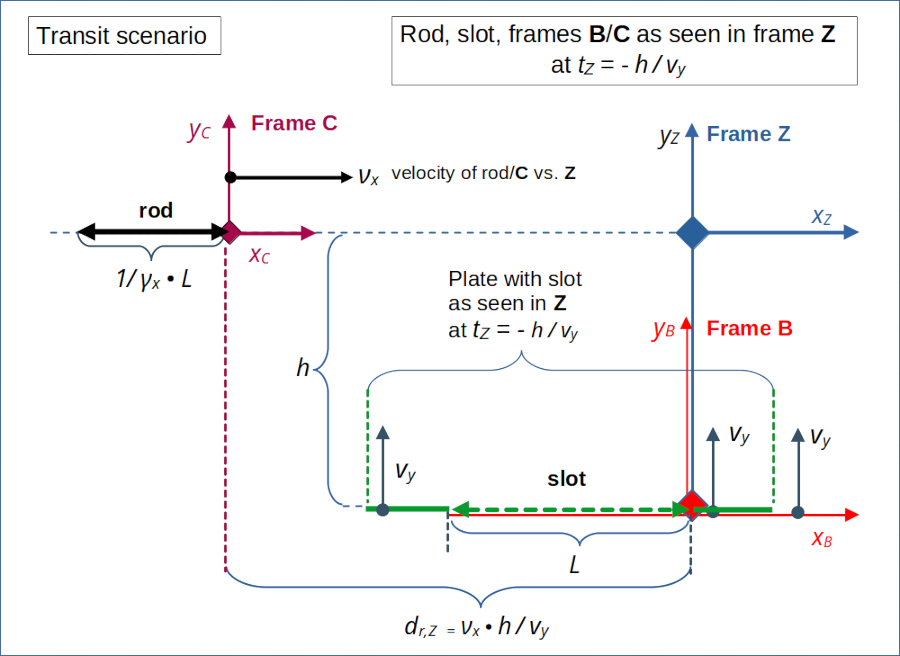
Setup of a "Transit Scenario" (horizontally moving rod, vertically moving slot)

Illustration 1: Setup of the “transit scenario” in reference frame Z. The rod moves horizontally with velocity –ν_x and its right end meets the the right end of slot, which moves upwards with velocity v_y, at the origin of frame Z at t_Z = 0. Frame C co-moves with the rod and frame B co-moves with the slot.

For details, notation and quantities see the previous posts in this series. We employ the usual β– and γ-factors characterizing the relative motion of inertial frame versus each other.

In post IX we have derived the results of the Lorentz Transformation for key event coordinates related to the rod’s and the slot’s end points at t_Z = t_C = 0 in the rod-attached frame C. The following schematic drawing displays some critical points in frame C and their motion during the transit (or equivantly the passage of the slot across the rod) :

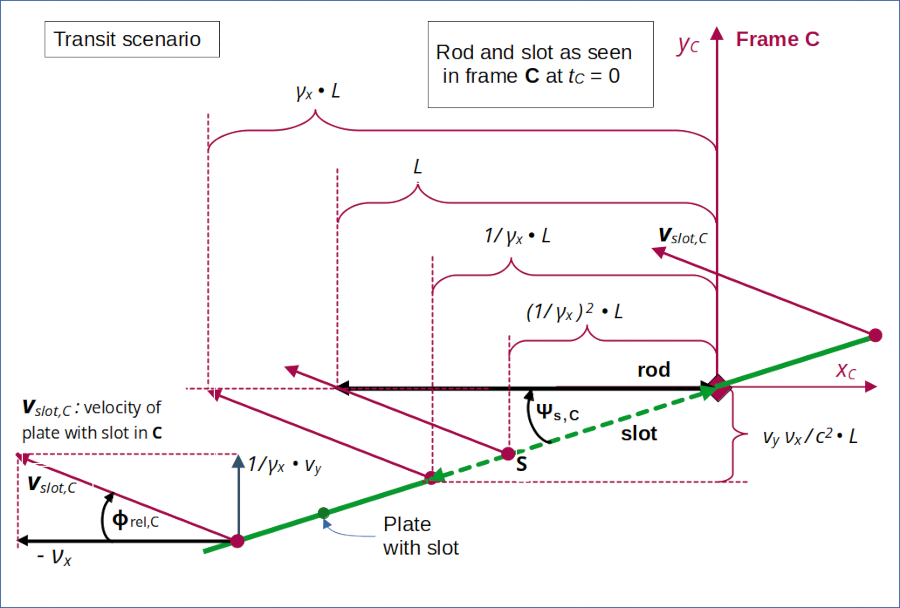
Details of rod/slot transit as seen by the rod

Illustration 2: Special points and distances in frame C at the start of the transit (= the slot passing the rod) without collision. The component of the slot’s velocity in y_C-direction in frame C differs from v_y (measured in frame A) due to time dilation effects.

Again, we observe a remarkable sequence of distances controlled by the γ-factor. Compare this to the results derived in the posts III and IV for the collision scenario.

In the last (9th) post we have already shown that the slot’s left end can be characterized by an event E2 at t_C=0:

\[ \mbox{slot’s left end at} \, t_C=0: \quad \left[\,x_C, \, y_C,\, t_C\,\right]_{E2,C} = \left[\, – \gamma_x *L, \,\,- \nu_x\,v_y / c^2, \,\, 0\,\right]_{E2,C} \,. \]

The length of the slot in C is calculated as

\[ \begin{align} L_{slot,C}^2 \,&=\, \left( {1 \over \gamma_x} \,L \right)^2 \,+\, \left( {\nu_x * v_y \over c^2}\,L \right)^2 \\[8pt] &= \, L^2 * \left[\, 1 \,-\, \beta_x^2 \left(\,1 – \beta_y^2\,\right)\, \right] \,. \end{align} \]

As a consequence we can describe the angle Ψ_s,C between the slot and the x_C-axis by the following relations:

\[ \begin{align} \tan\left(|\Psi_{s,C}|\right) \,&=\, \gamma_x \, { \nu_x * v_y \over c^2 }\,, \\[8pt] \cos \left(|\Psi_{s,C}|\right) \,&=\, {1 \over \gamma_x} L / L_{slot} \,, \\[8pt] \sin \left(|\Psi_{s,C}|\right) \,&=\, {\nu_x * v_y \over c^2} L / L_{slot} \,. \end {align} \]

We also have found that the left end of the slot reaches the line y_C = 0 at a point (x_C, y_C) = (- γ_x • L, 0)

\[ \mbox{slot’s left end at} \, y_C=0: \quad \left( x_C, \, y_C\right) = \left(\, – \gamma_x *L, \,\,0 \,\right) \,. \]

Let us also evaluate the movement of a point “S” on the slot with x_C-distance of γ_x² • L to the left of C‘s origin. The vertical distance Δy_S of this point to the line y_C = 0 at t_C = 0 is given by

\[ {\Delta y_S \over \gamma_x^{-2 } * L } \,=\, \gamma_x {\nu_x * v_y \over c^2} \,. \]

This means:

\[ \Delta y_S \,=\, {1 \over \gamma_x} \, {\nu_x * v_y \over c^2} * L \,. \]

The time Δt_S to cross this vertical distance is

\[ \Delta t_S \,= \, {\Delta y_s \over \gamma_x^{-1} v_y} \,=\, {\nu_x \over c^2 }\, L \,. \]

After this time interval the point S reaches the x_C-coordinate

\[ \begin{align} x_S \, &= \, – {1 \over \gamma_x^2} *L \,-\, \nu_x { \nu_x \over c^2} * L \\[8pt] &= \, – L * ( 1-\beta_x^2 + \beta_x^2) \,=\, L \,, \end{align} \]

as depicted in illustration 2.

Velocity of the slot and respective components

The velocity of the slot vs. the rod has two different components, namely v_s,x,C = – in x_C-direction and v_s,y,C in y_C-direction. We write this in “vector notation” as a vector v_slot,C

\[ \begin{align} \pmb{v}_{slot,C} \,&= \, \left(\, v_{s,x,C}, \,\, v_{s,y,C}\, \right) \, \\[8pt] &=\, \left( – \nu_x, \,\, {1 \over \gamma_x} v_y \,\right)\,. \end{align} \]

Pythagoras gives us the length of the vector and thus the absolute value of the velocity of the slot

\[ \begin{align} v_{slot,C} \,&= \, || \pmb{v}_{slot,C} || \\[8pt] &=\, \left( \, \nu_x^2 \,+\, \gamma_x^{-2}\, v_y^2 \,\right)^{-1/2}\,. \end{align} \]

The angle Φ_rel,C between the x_C-axis and the slot’s velocity is given by

\[ \tan \left( |\Phi_{rel,C}|\right) \,=\, {1 \over \gamma_x } \, {v_y \over \nu_x} \,. \]

Conclusion

The attentive reader has, of course, noticed that the above results for absolute values of distances and inclination angles in the rod’s frame of our transit scenario are completely analogous to similar results derived for the collision scenario (in the slot’s frame there).

This indicates already that a direct Lorentz Transformation e.g. from the rod’s frame C to the slot’s frame B will give us values consistent with the results of a LT between frame Z and frame B. This would prove full consistency between the descriptions of a collision-free transit of the rod through the slot by observers in frames Z, B and C. Thus, any potential paradox will disappear for the transit scenario, too.

The Lorentz Transformation between frame C to frame B will be the topic of the next post. We expect again a combination of spatial rotations and a 1-dimensional Lorentz transformation along the line of relative motion between the rod and the slot.

Stay tuned …