Special relativity and the rod/slot paradox – XIII – Lorentz transformation of the collision scenario to a diagonally moving frame

In this post series we now look a bit deeper into the rod/slot paradox of Einstein’s Theory of Special Relativity. We now want to compare our “collision scenario” and “transit scenario” directly and point out a major qualitative difference. This requires a transformation to a frame which makes such a direct comparison possible. In the previous post we have therefore prepared a transformation of our collision scenario from a setup frame A to a diagonally approaching frame W. Frame W was closely related to the frame Z which we used in this series to set up the transit scenario. (See below and previous posts.) W co-moves horizontally with the slot and vertically with the rod approaching the origin of the frame A used to define the collision scenario. The origins of W and A meet at t_W = t_A= 0.

In this post we apply a Lorentz Transformation [LT] to the physical objects of the collision scenario to get respective data in frame W. We continue to work on a rather elementary mathematical level.

We will find that both objects are perceived rotated with respect to the line of relative motion between the frames – in comparison to the situation given in A. There is also an angle between both objects when their left ends meet at the origin of W at local time t_W = 0. We will also see that in W the slot is oriented in parallel to the image of the x-axis of A and fully aligned with it at t_W = 0.

We use the abbreviations :
CCS : Cartesian coordinate system. LT: Lorentz Transformation.

Relation of frames W and A – and LT along the line of relative motion

For a better comparison of our two scenario we need the results of a LT of the coordinates of our physical objects from a setup frame A to a diagonally approaching frame W (closely related to the frame Z used for the transit scenario). We use a standard (and mathematically simple) boost along the line of relative motion of the frames. I.e.: We want to get the coordinates of the slot’s and rod’s end in an Cartesian coordinate system of W with an x_rel,W-axis aligned with the line of relative motion. We use results of the previous post.

In comparison to frame Z (for the transition scenario) the horizontal velocity of W is adapted such that the left ends of the rod and slot meet at t_A = t_W = 0, when also the origins of the frames coincide.

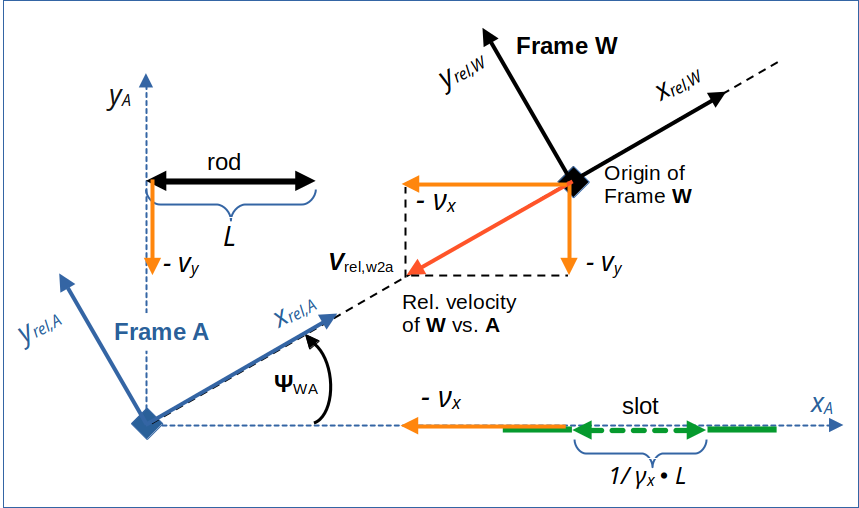
Rotated coordinate systems of frames A and W

Illustration 1: A diagonally approaching frame W in our collision scenario, which set up in a frame A. For a Lorentz Transformation from A to W we use rotated Cartesian coordinate systems with x-axes oriented along the line of relative motion of the frames.

To apply the boost along the line of relative motion we first transform velocity and position vectors to the rotated CCS in A at t_A = 0. We use the quantities, terms and abbreviations defined in the previous 12th post. Relativistic factors to be used along the line of relative motion are defined by:

\[ \begin{align} v_{rel}^2 \,&=\, v_{rel,w2a}^2 \,=\, \nu_x^2 \,+\, v_y^2 \,, \\[8pt] \beta_{rel}^2 \,&=\, \beta_{w2a}^2 \,=\, { 1 \over c^2}\, \left(\, \nu_x^2 \,+\, v_y^2 \,\right) \, =\, \beta_x^2 \,+\, \beta_y^2 \,, \\[8pt] \gamma_{rel}^2 \,&=\, \gamma_{w2a}^2 \,=\, {1 \over 1 \,-\ \beta_{w2a}^2 } \,=\, {1 \over 1 \,-\ \beta_x^2 \,-\, \beta_y^2} \,. \end{align} \]

We sometimes use “rel” as a subscript instead of “w2a” to indicate velocities along the line of relative motion of the frames and coordinates along this line.

It is clear that at time t_A= t_W = 0 the left ends of the slot and the rod meet at the origins of A and W, which coincide at this point in time:

\[ \begin{align} t_A = t_W &= 0: \\[8pt] x_{s,l,rel,A} \,&=\, x_{s,l,rel,W} \,=\, 0\,, \quad y_{s,l,rel,A} \,=\, y_{s,l,rel,W} \,=\, 0 \,, \\[8pt] x_{r,l,rel,A} \,&=\, x_{r,l,rel,W} \,=\, 0\,, \quad y_{r,l,rel,A} \,=\, y_{r,l,rel,W} \,=\, 0 \,. \end{align} \]

Event coordinates for the slot’s right end in A

Regarding the right end of the slot we have to focus on an event which gets transformed to the specific point in time t_W = 0 in W. This ensures that we get x/y-coordinates (of both of the slot’s ends) which an observer in W measures simultaneously, namely at t_W = 0.

In the rotated CCS of W a LT gives us the following transformed time coordinate (see the 3rd post)

\[ \begin{align} t_{s,r,rel,W} \, &=\, \gamma_{rel} \, \left[ \, t_{s,r,rel,A} \,+\, { v_{rel} \over c^2} \, x_{s,r,rel,A} \,\right] \,=\, 0 \, \Rightarrow \\[8pt] t_{s,r,rel,A} \, &=\, -\, { v_{rel} \over c^2} \, x_{s,r,rel,A} \,. \end{align} \]

The reader of the previous posts recognizes this returning pattern.

Event coordinates of the right end of the slot in the rotated CCS of A

Due to the purely horizontal movement of the slot in A the x_A-coordinate value x_s,r,A of the slot’s right end on the standard x_A-axis has to be changed from its value at t_A = 0

\[ t_A = 0: \quad x_{s,r,A}(0) \,=\, {1\over \gamma_x} \, L \]

\[ \begin{align} x_{s,r,A}(t_{s,r,rel,A}) \,&=\, {1 \over \gamma_x}\, L \,+\, (-\,\nu_x) * \left(\,t_{s,r,rel,A} \,-\, 0\right) \\[8pt] &=\, {1 \over \gamma_x}\, L \,-\,\nu_x * t_{s,r,rel,A} \,. \end{align} \]

The respective coordinate x_s,r,rel,A in the rotated CCS is found by a projection on the relative line of motion:

\[ \begin{align} x_{s,r,rel,A} \, &=\, \cos \left(\Psi_{WA} \right) * \left[\, {1 \over \gamma_x}\, L \,-\,\nu_x * t_{s,r,rel,A} \,\right] \\[8pt] &=\, {\nu_x \over v_{rel}} * \left[\, {1 \over \gamma_x}\, L \,-\, \nu_x * t_{s,r,rel,A} \,\right] \,. \end{align} \]

For the time t_s,r,rel,A (to be chosen) we therefore get the condition:

\[ \begin{align} &t_{s,r,rel,A} \, =\, -\, { v_{rel} \over c^2} \, {\nu_x \over v_{rel}} * \left[\, {1 \over \gamma_x}\, L \,-\, \nu_x * t_{s,r,rel,A} \,\right] \Rightarrow \\[8pt] &t_{s,r,rel,A} \,\left[\, 1 \,-\, {\nu_x \over c^2}\,\right] \, =\, – {1 \over c} \, {1 \over \gamma_x} \, \beta_x \,L \,, \\[8pt] &t_{s,r,rel,A} \,\left[\, 1 \,-\, \beta_x^2 \,\right] \,=\, t_{s,r,rel,A} * {1\over \gamma_x^ 2} \,=\, – {1 \over c} \, {1 \over \gamma_x} \, \beta_x \,L \,, \\[8pt] &t_{s,r,rel,A} \,=\, – {1\over c} \, \gamma_x\, \beta_x \, L \,. \end{align} \]

From this point in time we get the x_A-coordinate of the slot’s right end at time t_s,r,rel,A:

\[ \begin{align} x_{s,r,A} \left( t_{s,r,rel,A} \right) \,&=\, {1 \over \gamma_x} \, L \,+\, \nu_x \,{1 \over c}\, \gamma_x\beta_x\,L \\[8pt] &=\, {1 \over \gamma_x} \, L \,\left( \, 1 \,+\, \beta_x^2 \,\gamma_x^2\, \right) \\[8pt] &= \, {1 \over \gamma_x} \, L \, \gamma_x^2 \, = \, \gamma_x \, L \,. \end{align} \]

The respective x_rel,A-coordinate in the rotated CCS is:

\[ \begin{align} x_{s,r,rel,A} \,&=\, \cos \left( \Psi_{WA} \right) * x_{s,r,A} \left( t_{s,r,rel,A} \right) \,\Rightarrow \\[8pt] &=\, \gamma_x \, { \nu_x \over v_{rel}} \, L \,=\, \gamma_x \, {\beta_x \over \beta_{rel}} \,. \end{align} \]

The respective y_rel,A-coordinate in the rotated CCS is given by

\[ \begin{align} y_{s,r,rel,A} \,&=\, – \, x_{s,r,A} \left( t_{s,r,rel,A} \right) * \sin \left( \Psi_{WA} \right) \, \Rightarrow \\[8pt] &=\, – \, \gamma_x \, L \, {v_y \over v_{rel}} \,=\, -\, \gamma_x \, \, {\beta_x \over \beta_{rel} } \, L \,. \end{align} \]

We now have all necessary data in A to perform the boost along the line of relative motion to our (rotated) coordinate system of W for the point in time t_W = 0.

\[ x_{s,r,rel,A} \,=\, \gamma_x \, {\beta_x \over \beta_{rel} }\, L \,, \quad y_{s,r,rel,A} \,=\, -\, \gamma_x \, \, {\beta_x \over \beta_{rel} } \, L \,, \quad t_{s,r,rel,A} \,=\, – {1\over c} \, \gamma_x \, \beta_x \, L \,. \]

Lorentz Transformation of slot data to W

We transform x_s,r,rel,A by the standard boost along the line of relative motion:

\[\begin{align} x_{s,r,rel,W} \, &= \, \gamma_{rel} \,\left[\, x_{s,r,rel,A} \,+\, v_{rel} \, x_{s,r,rel,A} \,\right] \\[8pt] &= \, \gamma_{rel} \,\left[\, \gamma_x \, {\beta_x \over \beta_{rel} } \, L \,-\, v_{rel} * {1\over c^2} \, \gamma_x \, \beta_x \, L\, \,\right] \\[8pt] &= \, \gamma_{rel} \, \gamma_x \, \beta_x \, L \, \left[\, {1 \over \beta_{rel} } \, -\, \beta_{rel} \, \right] \\[8pt] &= \, \gamma_{rel} \, \gamma_x \, \beta_x \, L \, {1 \over \beta_{rel}} \, \left( \, 1 \,-\, \beta_{rel}^ 2\,\right) \\[8pt] &= \, {\gamma_x \over \gamma_{rel}} \, {\beta_x \over \beta_{rel} } \, L \,. \end{align}\]

So,

\[ x_{s,r,rel,W} = \, {\gamma_x \over \gamma_{rel}} \, {\beta_x \over \beta_{rel} } \, L \,\lt\, L \,. \]

You can also check that

\[ \begin{align} y_{s,r,rel,W} \,&= \, -\, \gamma_x \, \, {\beta_x \over \beta_{rel} } \, L \,, \\[8pt] t_{s,r,rel,W} \,&=\, \, \gamma_{rel} \, \left[ \, t_{s,r,rel,A} \,+\, { v_{rel} \over c^2} \, x_{s,r,rel,A} \,\right] \\[8pt] &=\gamma_{rel} \, \left[ – {1\over c} \, \gamma_x \, \beta_x \, L \, – \, { v_{rel} \over c^2} \, \gamma_x \, {\beta_x \over \beta_{rel}}\,L \,\right] \,=\,0 \,. \end{align}\]

Length of the slot in the diagonally moving frame W

We get the resulting length of the slot by applying Pythagoras to the data given at t_W = 0. Remember that at this point in time the left ends of the rod as well as of the slot coincide with the origins of A and W.

\[ \begin{align} L_{slot,W}^2 \,&=\, {\gamma_x^2 \over \gamma_{rel}^2} \, {\beta_x^2 \over \beta_{rel}^2} \, L^2 \,+\, \gamma_x^2 {\beta_y^2 \over \beta_{rel}^2} \, L^2 \\[8pt] &= \, \gamma_x^2 \,{ 1 \over \beta_{rel}^2 } \, L^2 \left[\, {\beta_x^2 \over \gamma_{rel}^2} \,+\, \beta_y^2 \,\right] \\[8pt] &= \, {\gamma_x^2 \over \gamma_{rel}^2} \,{ 1 \over \beta_{rel}^2 } \, L^2 \left[\, \beta_x^2 \,+\, \gamma_{rel}^2 \, \beta_y^2 \,\right] \\[8pt] &= \, {\gamma_x^2 \over \gamma_{rel}^2} \,{ 1 \over \beta_{rel}^2 } \, L^2 \left[\, \beta_x^2 \,+\, {1 \over 1 – \beta_x^2 – \beta_y^2} \, \beta_y^2 \,\right] \\[8pt] &= \, \gamma_x^2 \,{ 1 \over \beta_{rel}^2 } \, L^2 \left[\, \beta_x^2 (1 – \beta_x^2) \,+\, \beta_y^2 \, (1 – \beta_x^2) \,\right] \\[8pt] &= \,{ 1 \over \beta_{rel}^2 } \, L^2 \left[\, \beta_x^2 \,+\, \beta_y^2 \,\right] \,\, \Rightarrow\\[8pt] L_{slot,W}^2 \,&=\, L^2 \,, \quad L_{slot,W} \,=\, L \,. \end{align}\]

Not too surprising – if you dwell a bit on it.

Angle between the slot in W and the line of relative motion

The slot resides below the line of relative motion in W – due to the negative y_s,r,rel,W-coordinate of its right end. So, we get the angle Ψ_s,rel,W between the slot and the line of relative motion by

\[ \cos \left(| \Psi_{s,rel,W} |\right) \,=\, {x_{s,r,rel,W} \over L} \,=\, {\gamma_x \over \gamma_{rel} } \, {\beta_x \over \beta_{rel}} \,. \]

Remember

\[ \cos \left(| \Psi_{WA} |\right) \,=\, \cos \left(| \Psi_{s,rel,A} | \right) \,=\, {\beta_x \over \beta_{rel}} \,. \]

Therefore

\[ \begin{align} &\cos \left(| \Psi_{WA} |\right) \,=\, \cos \left(| \Psi_{s,rel,A} | \right) \,\lt\, \cos \left(| \Psi_{s,rel,W} | \right) \,\,\Rightarrow \\[8pt] &\Psi_{s,rel,W} \,\gt\, \Psi_{WA} = \Psi_{s,rel,A} \,. \end{align} \]

For the last inequality we have assumed that the angles have the same positive orientation.

The interesting thing (but to be expected) thing is now that Ψ_s,rel,W is identical to the angle of the image x_xA,W of the standard x_A-axis (of A) with the line of relative motion in W (see the results of the previous 12th post):

\[ \cos(\Psi_{xA,W}) \,=\, {\gamma_x \over \gamma_{rel} } \, {\beta_x \over \beta_{rel}} \,=\, \cos \left( \Psi_{s,rel,W} \right) \]

The angle between the slot and line of relative motion is bigger in W than the corresponding angle in frame A and is equal to the angle of the image x_xA,W with the line of relative motion. Both appear rotated outward in comparison to the situation in the original frame A.

We saw something qualitatively similar when we discussed the angle of the x_C-axis vs. the line of relative (diagonal) motion of frame C vs. frame B in the 4th and 5th posts of this series.

Conclusion

In this post we have derived the coordinates of the slot relative to a coordinate system of W with an x-axis aligned with line of relative motion (of W vs. frame A). We found that the length of the slot in W is identical to its proper length L (at rest). Furthermore the slot aligns with the transformation’s image of the x_A-axis of frame A in W . We will later see that this result was to be expected. In frame W the angle between the slot and the line of relative motion is bigger than in frame A. This reflects a rotation outward due to relativistic effects.

In the forthcoming posts we will have look at further details of the situation in W at time t_W = 0. Th etopic of the next post is a Lorentz Transformation of the rod to our diagonally moving frame W:

Special relativity and the rod/slot paradox – XIV – angle between colliding rod and slot in a diagonally moving frame

Later on we will analyze the transformed velocity vectors of both the slot and the rod. One result will be that the velocity vector of the slot is perpendicular to the slot’s orientation in W – as it should be according to other theoretical considerations.

Stay tuned …