Special relativity and the rod/slot paradox – XI – Lorentz Transformation between slot and rod for the transit scenario

In our post series about the rod/slot “paradox” in Special Relativity we presently study a “transit scenario”. In this scenario the rod passes the slot unharmed due to a clever combination of initial conditions in a setup frame Z. We have already studied the Lorentz Transformation [LT] of key event coordinates from the setup frame Z to a reference frame C co-moving and aligned with the rod. Observers in both frames consistently agree upon the fact that the rod moves through the slot without a collision with the slot-surrounding plate. But to make any potential paradoxes disappear we yet have to prove that a direct Lorentz Transformation [LT] between a frame B co-moving with the slot to the rod’s frame C also produces consistent transit results. Performing such a LT is the endeavor of this post.

Working plan

We closely follow the steps we have already learned in the context of the collision scenario, but apply them to the transit scenario. Note that both rod and slot have a proper length L. The reduced length of the rod assumed in frame Z is due to the relativistic length contraction.

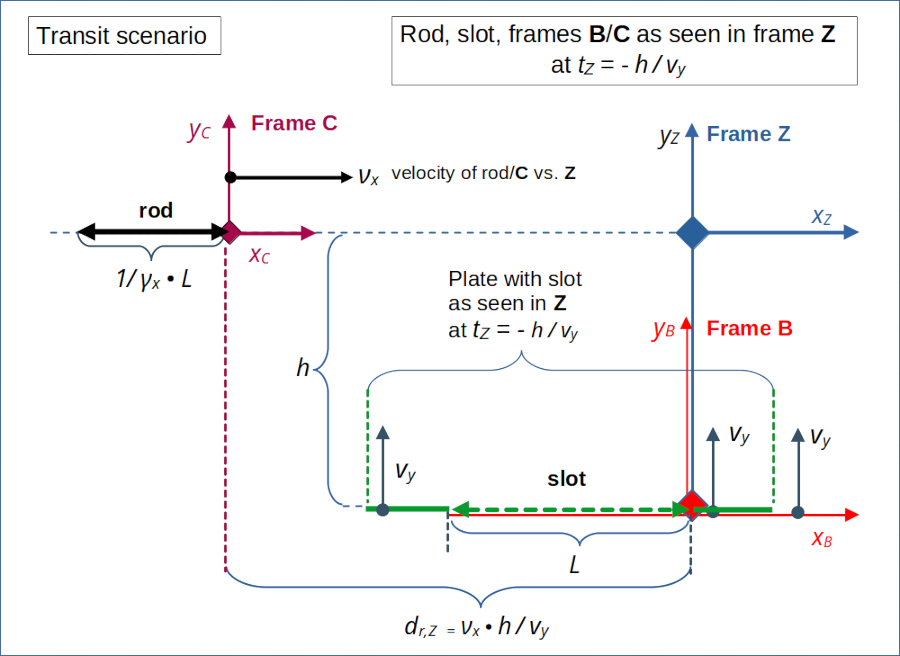
Setup of a "Transit Scenario" (horizontally moving rod, vertically moving slot)

Illustration 1: Setup of the “transit scenario” in reference frame Z. For details see the previous posts. Both rod and slot have a proper length of L at rest in their attached frames C and B, respectively. In frame Z the length of the rod is measured to be 1 / γ_x • L due to relativistic length contraction.

We first establish the perception of an observer in the slot’s frame B. We write down the components of the relative velocity between the rod and the slot.
We calculate the inclination angle of the velocity vector with the x-axes of frames B and C. We expect these angles to be different due to the impact of time dilation.
Afterward we project spatial position vectors onto the line of relative motion in frame B. This process is equivalent to a spatial rotation of the spatial Euclidean coordinate system [ECS] of B with the x-axis of the rotated ECS coinciding with the line of relative motion. The projection gives us the spatial coordinates in the rotated spatial ECS.
We apply a 1-dimension Lorentz Transformation between the rotated ECS in B and a similarly rotated ECS attached to the rod in C. This LT is completely controlled by the absolute value of the relative velocity between the rod and the slot.
Eventually, we calculate and check inclination angles vs. the x_C-axis and values for the rod/slot lengths resulting from the transformed slot’s and rod’s end point coordinates in the rod’s frame C.

Perception of the rod’s transit by an observer in the slot’s frame

The perception of an observer in frame B is relatively easy to derive as the relative motion between frame B and frame Z occurs along the y_Z-axis of frame Z. The relative velocity of B vs. Z is –v_y.The orientation of the rod and the slot is vertical to the line of the relative motion of the slot vs. Z. Therefore, the lengths of the rod and slot are not affected by any (further) length contraction effects. The x-coordinates of the end-points of these objects are not changed by a LT along the y-axes for a given point in time and related events. To perform the LT we just have to interchange the meaning of x- and y-axes in the standard formulas of the Lorentz Transformation [LT] (given in post III). The rod will be measured by an observer in B to have the same length as measured in Z. Also the orientation of the rod vs. the x-axis will not change by the LT from Z to B.

However, time dilation between Z and B has an impact on the transformation of the velocity of the rod (measured in Z as ν_x) from frame Z to B. An observer in B will measure a reduced velocity v_r,x,B = 1 / γ_y • ν_x.

\[ \begin{align} &\mbox{rod’s velocity component in x-direction in B : } \\[8pt] & \quad v_ {r,x,B} \,=\, { 1 \over \gamma_y} * \nu_x \,. \end{align} \]

The relative vertical velocity component of the rod vs. the slot is, of course, –v_y :

\[ \begin{align} &\mbox{rod’s velocity component in y-direction in B : } \\[8pt] & \quad v_ {r,y,B} \,=\, – v_y \,. \end{align} \]

Let us write down the spatial components of the relative velocity vector v_rod,B of the rod vs. the slot as seen by the slot in our simple vector notation (v_r,x,B, v_r,y,B). The bold v indicates a vector :

\[ \begin{align} \pmb{v}_{rod,B} &= \left( \, v_{r,x,B}, \,\, v_{r,y,B} \,\right) \\[8pt] &=\, \left( {1 \over \gamma_y} \, \nu_x, \,\, – v_y\,\right) \,. \end{align} \]

This, of course, is also the relative velocity v_rel,CB of frame C vs. frame B as seen by an observer in frame B

\[ \pmb{v}_{rel,CB} \,=\, \pmb{v}_{rod,B} \,. \]

The length of the slot in frame B obviously is L, and the length of the rod remains 1 / γ_x • L after the LT to frame B. We arrive at the following drawing which characterizes the transit perception of an observer in B at t_B = t_Z = 0:

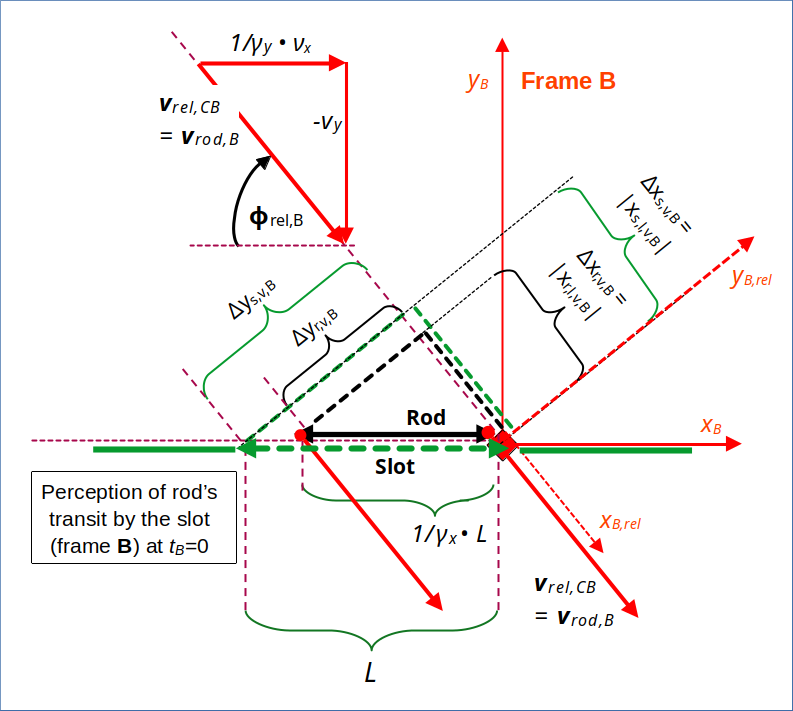
Transit scenario seen from the perspective of the slot

Illustration 2: Perception of the transit by an observer in frame B co-moving with the slot. The rod approaches diagonally and moves through the slot at t_B = 0. This is the last possible moment for the transit of infinitesimally thin objects. Note that the rod has the same contracted length in frame B as in Z. A rotated ECS is indicated by the dotted axes named x_B.rel and y_B,rel.

Due to our timing of the rod/slot encounter, the transit of the rod occurs at the last possible moment. We have assumed infinitesimally thin objects in y_Z– (and z_Z-) direction. The drawing displays projections of the slot and the rod onto the line of relative movement as seen in frame B. The angle Φ_rel,B between the x_B-axis and the rod’s velocity is given by

\[ \tan \left( |\Phi_{rel,B}|\right) \,=\, { v_y \over \gamma_y^{-1} \nu_x } \, = \gamma_y * {v_y \over \nu_x} \,. \]

We know already that it is different from the corresponding angle Φ_rel,C in frame C (see below and the previous 9th post of this series):

\[ { \tan \left( |\Phi_{rel,B}|\right) \over \tan \left( |\Phi_{rel,C}|\right) } \,=\, \gamma_x * \gamma_y \,. \]

See the 5th post of this series for a corresponding (inverse) relation for the collision scenario – and note that frames B and C have changed roles.

Different inclination angles of the relative velocity vector to the x-axes of the rod/slot frames

Before we apply a LT from frame B to C let us gather some more information about the transit scenario. We remember the results of the LT from Z to C (see post X):

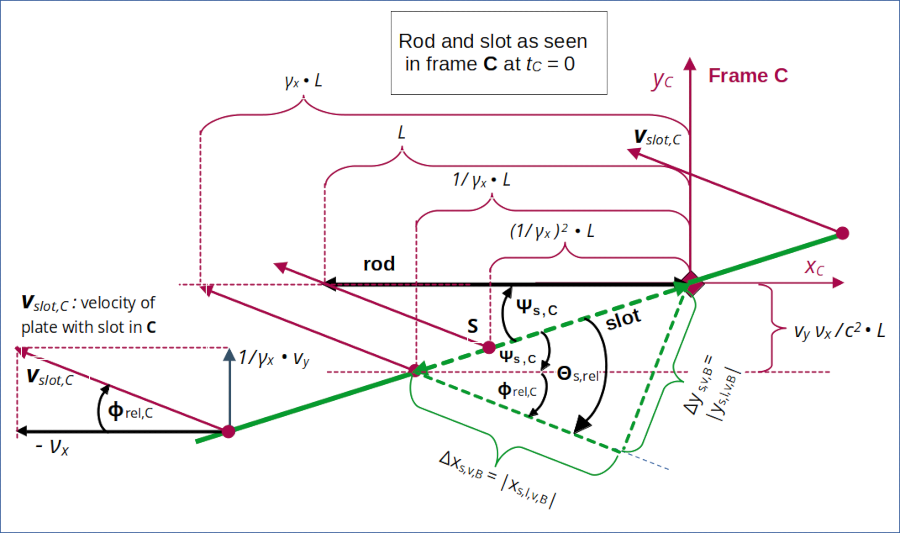
Details of rod/slot transit as seen by the rod

Illustration 3: Perception of the transit scenario by the rod – according to a LT from frame Z to frame C. See post X for details.

The absolute value of the relative velocity is given in our frames C and B by

\[ v_{rel,BC} = || \pmb{v}_{slot,C} || \,, \quad v_{rel,CB} = || \pmb{v}_{rod,B} || \,. \]

It is easy to show that these velocity values are identical:

\[ \begin{align} v_{rel} \, & := \, v_{rel,CB} \,=\, v_{rel,BC} \\[8pt] &= \, \left( \, \nu_x^2 \,+\, \gamma_x^{-2}\, v_y^2 \,\right)^{-1/2} \\[8pt] &= \, \left( \, v_y^2 \,+\, \gamma_y^{-2}\, \nu_x^2 \,\right)^{-1/2} \,. \end{align} \]

We also know

\[ \gamma_{rel,BC} = \left[1 – {v_{rel,BC} \over c^2} \right]^{-1/2} \,=\, \gamma_ {rel,CB} = \left[1 – {v_{rel,CB} \over c^2} \right]^{-1/2} \]

with

\[ \gamma_{rel,BC} = \gamma_ {rel,CB} =: \gamma_x * \gamma_y \,. \]

Cosine and sine values for Φ_rel,B and Φ_rel,Care given by :

\[ \begin{eqnarray*} & \pmb{\operatorname{B : }} \quad &\cos (|\Phi_{rel,B}|) \,=\, {1 \over \gamma_y} { \nu_x \over v_{rel}}, &\quad \sin (|\Phi_{rel,B}|) \,=\, {v_y \over v_{rel}} \,, \\[8pt] & \pmb{\operatorname{C : }} \quad &\cos (|\Phi_{rel,C}|) \,=\, {\nu_x \over v_{rel}}, &\quad \sin (|\Phi_{rel,C}|) \,=\, {1 \over \gamma_x} {v_y \over v_{rel}} \,. \end{eqnarray*} \]

The length of the slot in frame C has been found (see the previous 10th post to be given as

\[ L_{slot,C}^2 \,=\, \, L^2 * \left[\, 1 \,-\, \beta_x^2 \left(\,1 – \beta_y^2\,\right)\, \right] \,. \]

The angle of the slot with the x_C-axis is given by

\[ cos \left(|\Phi_{s,C} |\right) \,=\, {1 \over \gamma_x} {L \over L_{slot,C}} \,. \]

These values should be reproduced by a direct LT from frame B to C.

Lorentz Transformation of the slot’s coordinates from frame B to frame C

We start with the transformation of the slot’s end point coordinates. In B the slot does not move. We need the coordinates of the outer left end-points of the projection of the slot onto the line of relative motion (of the rod) in B. This line segment is parallel to the line of motion and the relative velocity v_rel,CB. The x-coordinate value x_s,l,v,B of its left end-point in the rotated ECS is

\[ \begin{align} x_{s,l,v,B} \,&=\, – \, \cos\left(|\Phi_{rel,B}|\right) * L \\[8pt] &= \, – \, {1 \over \gamma_y} {\nu_x \over v_{rel}} * L \,. \end{align} \]

The projected line segment vertical to the line of relative motion has an end-point at the coordinate y_s,l,v,B (in the rotated ECS), which is given by

\[ \begin{align} y_{s,l,v,B} \,&=\, – \, \sin\left(|\Phi_{rel,B}|\right) * L \\[8pt] &= \, – \, {v_y \over v_{rel}} * L \,. \end{align} \]

The lengths of both line segments are given by the absolute values of the endpoint coordinates:

\[ \begin{align} \Delta \,x_{s,v,b} \,&=\, | x_{s,l,v,b}| \,,\\[8pt] \Delta \,y_{s,v,b} \,&=\, | y_{s,l,v,b} |\,. \end{align} \]

The LT with v_rel along the line of motion to frame C leads to a simple length contraction, because the slot is at rest in B. You can derive this in detail via the LT formulas of the 3rd post. We take a shortcut here. The corresponding result for the transformed coordinates is:

\[ \begin{align} x_{s,l,v,C} \,&= \,-\, {1 \over \gamma_x * \gamma_y } {1 \over \gamma_y} {\nu_x \over v_{rel}} * L \,, \\[8pt] \Delta \, x_{s,v,C} \,&=\, |x_{s,l,v,C} | \,. \end{align} \]

The projected vertical line segment remains of course unchanged by a LT between coordinate systems with x-axis along the line of relative motion:

\[ \begin{align} y_{s,l,v,C} \,&=\, y_{s,l,v,B} \,= \,- \, {v_y \over v_{rel}} * L \,, \\[8pt] \Delta \, y_{s,v,C} \,&=\, |y_{s,l,v,C} | \,. \end{align} \]

From these data we can calculate the length of the slot in frame C as given by the LT:

\[ \begin{align} L_{slot,C,LT} \,&=\, \left[\, \left( {v_y\over v_{rel}} \right)^2 \,+\, \left( {1 \over \gamma_x * \gamma_y} \right)^2 \,\left( {1\over \gamma_y} \right)^2 \,\left( {\nu_x\over v_{rel}} \right)^2\,\right] * L^2 \\[8pt] &= \, \left[\, \left( {v_y\over v_{rel}} \right)^2 \,+\, \left(1 – {v_{rel}^2 \over c^2}\right) \, {1\over \gamma_y^2} \,\left( {\nu_x\over v_{rel}} \right)^2 \,\right] * L^2 \\[8pt] &= \, \left[\, \left( {v_y\over v_{rel}} \right)^2 \,+\, {1\over \gamma_y^2} \, \left( {\nu_x \over v_{rel}} \right)^2 \,-\, {1\over \gamma_y^2} \, \left( {\nu_x\over c} \right)^2 \,\right] * L^2 \\[8pt] &= \, \left[ \, 1 \,-\, \beta_x^2 \,\left( 1 \,-\, \beta_y^2\right) \,\right] * L^2 \,. \end{align} \]

Hence

\[ L_{slot,C,LT} \,=\, L_{slot,C} \, \lt L \,. \]

Good! What about the angle of the slot Ψ_s,C with the x-axis according to the LT? In frame C we have to calculate the angle by the following formula (see illustration 2):

\[ \begin{align} \cos \left(| \Psi_{s,C}|\right) \,&=\, \cos \left(|\Theta_{s,rel} | \,-\, |\Phi_{rel,C}| \right) \\[8pt] &= \, \cos \left(|\Theta_{s,rel}|\right) * \cos \left(|\Phi_{rel,C}|\right) \,+\, \sin \left(|\Theta_{s,rel}|\right) * \sin \left(|\Phi_{rel,C}|\right) \,. \end{align} \]

The angle Θ_s,rel is the angle between the slot and the line of relative motion. It is given by

\[ \begin{align} \cos \left(|\Theta_{s,rel}| \right) \,&=\, {\Delta \, x_{s,v,C} \over L_{slot,C} } \\[8pt] & = \, {1 \over \gamma_x * \gamma_y } {1 \over \gamma_y} {\nu_x \over v_{rel}} * {L \over L_{slot,C}} \,, \\[10pt] \sin \left(|\Theta_{s,rel}| \right) \,&=\, { \Delta \, y_{s,v,C} \over L_{slot,C} } \\[8pt] & = \, {v_y \over v_{rel}} * { L \over L_{slot,C} } \,. \end {align} \]

With the other values given above we get

\[ \begin{align} \cos \left(| \Psi_{s,C}|\right) \,&=\, { L \over L_{slot,C}} * \left[ \, {1 \over \gamma_x} \,{1 \over \gamma_y^2} {\nu_x \over v_{rel}} \,+\, {1 \over \gamma_x} \,{v_y \over v_{rel}} \, \right] \\[8pt] &= \, {1 \over \gamma_x} \, {L \over L_{slot,C} } * \left[ \,{1 \over v_{rel}^2} \,\left( {1 \over \gamma_y^2} \, \nu_x^2 \,+\, v_y^2 \right) \,\right] \\[8pt] &= \, {1 \over \gamma_x} \, {L \over L_{slot,C} } \,. \end{align} \]

Which is correct! We have reproduced the length and the inclination angle which we previously found by a LT from frame Z to frame C. The slot appears rotated in frame C and its total length is somewhat shorter than L.

So, a LT from B to C transforms our key coordinate values for the slot just as we expected it from our setup. The measurements in Z, B, C for the slot’s length and orientation are fully consistent.

Lorentz Transformation of the rod’s coordinates from frame B to frame C

For the transformation of the rod we proceed almost analogously. But this time we have to take care of the fact that the rod moves. So we need to find the coordinates of an event which transforms its time coordinate to t_C = 0. The standard projection gives:

\[ \begin{align} x_{r,l,v,B} \,&= \, -\, \cos\left(|\Phi_{rel,B}|\right) * {1 \over \gamma_x} * L \\[8pt] &= \, – \, {1 \over \gamma_x * \gamma_y} {\nu_x \over v_{rel}} * L \,, \\[10pt] \Delta \, x_{r,v,B} \,&= \, |x_{r,l,v,B}| \,. \end{align} \]

And:

\[ \begin{align} y_{r,l,v,B} \,&=\, – \, \sin \left(|\Phi_{rel,B}|\right) * L \\[8pt] &= \, – \,{1 \over \gamma_x} {\nu_y \over v_{rel}} * L \,, \\[10pt] \Delta \, y_{r,v,B} \, &= \, |y_{r,l,v,B}| \,, \end{align} \]

A short calculation tells us the corrected t_B– and x_B-coordinates, t_r,l,v,B2 and x_r,l,v,B2, respectively, for the rod’s left end to fulfill

\[ t_{r,l,v,C} \,=\, 0 \quad \Rightarrow \quad t_{r,l,v,B2} \,=\, {v_ {rel} \over c^2} \, x_{r,l,v,B2} \,. \]

On the other side – due to the movement of the rod with v_rel along the line of relative motion:

\[ x_{r,l,v,B2} \,= \, x_{r,l,v,B} + v_{rel} * {v_ {rel} \over c^2} \, x_{r,l,v,B2} \]

Hence

\[ x_{r,l,v,B2} \,= \, \gamma_x^2 * \gamma_y^2 * x_{r,l,v,B} \,. \]

Thus, at t_C= 0, we get via the LT :

\[ \begin{align} x_{r,l,v,C} \,&=\, \gamma_x * \gamma_y * \left[\, \gamma_x^2\, \gamma_y^2 * x_{ r,l,v,B} – v_{rel} * {v_{rel} \over c^2} * \gamma_x^2 \, \gamma_y^2 * x_{r,lv,B} \, \right] \\[8pt] &=\, \gamma_x * \gamma_y * x_{ r,l,v,B} * \gamma_x^2 \, \gamma_y^2 * \left[\, 1 – {v_{rel} \over c^2} \,\right] \\[8pt] &= \, – \, \gamma_x * \gamma_y * \,{1 \over \gamma_x * \gamma_y}* {\nu_x \over v_{rel}} * L \,, \\[8pt] &= \, – {\nu_x \over v_{rel}} * L \,\,, \\[10pt] y_{r,l,v,C} \,&= \, \, – \,{1 \over \gamma_x} {\nu_y \over v_{rel}} * L \,. \end{align} \]

And:

\[ \begin{align} \Delta \, x_{r,v,C} \,&= \, |x_{r,l,v,C}| \,, \\[8pt] \Delta \, y_{r,v,C} \,&= \, |y_{r,l,v,C}| \,. \end{align} \]

For the rod’s length in C, as given by the LT, we get:

\[ \begin{align} L_{rod,C,LT}^2 \,&=\, (\Delta \, x_{r,v,C})^2 + (\Delta \, y_{r,v,C})^2 \\[8pt] &= \, L^2 * {1 \over v_{rel}^2} * \left( \nu_x^2 \,+\, {1\over \gamma_x^2}\, v_y^2 \right) \\[8pt] &= L^2 \,. \end{align} \]

And for the angle with the x_C-axis :

\[ \begin{align} \cos \left(|\Theta_{r,C}|\right) \, &= \, {\nu_x \over v_{rel}} \, {L \over L_{r,C} } = {\nu_x \over v_{rel} } \\[8pt] &= \, \cos\left(| \Phi_{rel,C}|\right) \quad \Rightarrow \\[8pt] \Psi_{r,C} \, &=\, 0 \,. \end{align} \]

This is exactly what we should get (according to a previous LT between frames Z and C)!

Direct Lorentz Transformation from frame C (rod) to frame B (slot)

The LT from frame B to frame C can be done analogously. I leave this to the reader. See also the calculation steps in similar posts for the collision scenario. Eventually, the LT from C to B will give you consistent data.

Conclusion – no paradox for the “transit scenario”

What have we shown for our “transit scenario”? We proved that LTs from the setup frame Z to frames B (co-moving with the slot) and C (co-moving with the rod) provided event data and spatial coordinates consistent with the data of direct LTs from frame B to frame C and vice versa.

All observers in all critical frames tell us the same message: If the rod moves through the slot in one frame, observers in other inertial frame will also find a smooth, collision-free transit. There is no paradox for the transit scenario! Just as there was no paradox for the collision scenario, which we analyzed in the first posts of this series.

The next and last post in this series will summarize our results for both of the rod/slot encounter scenarios we have studied. I will point out that our selected scenarios, though seemingly similar, reflect very different initial conditions. We will discuss why the order of certain symmetry operations and a related non-commutativity is crucial. This will lead us to the deeper causes of rod/slot “paradoxes” – namely a false representation of the initial conditions leading to a comparison of incompatible scenarios.