Up to now we have analyzed the “rod / slot paradox” in Special Relativity [SR] via a well defined “collision scenario”. The results of Lorentz Transformations [LT] between various reference frames showed no paradox at all. Instead we got consistent descriptions between different observers, e.g. between an observer co-moving with the rod and an observer co-moving with the slot. We now start to investigate a scenario in which the rod moves through the slot; let us call it the “transit scenario“.

In subsequent posts we will find out what the perceptions of observers in different reference frames look like for the transit of the rod through the slot. We will again see that their measurements differ concerning lengths, inclination angles and space as well as time coordinates of key events. But all observers will agree upon the fact that the rod passes the slot unharmed.

Previous posts:

• Post I: Special relativity and the rod/slot paradox – I – seeming contradictions between reference frames
• Post II: Special relativity and the rod/slot paradox – II – setup of a collision scenario
• Post III: Special relativity and the rod/slot paradox – III – Lorentz transformation causes inclination angles
• Post IV: Special relativity and the rod/slot paradox – IV – consequences of an inclination angle in the slot’s frame
• Post V: Special relativity and the rod/slot paradox – V – perspective of the rod and aspects of the relative velocity between the rod and the slot
• Post VI: Special relativity and the rod/slot paradox – VI – consistency and the Lorentz Transformation between the slot and the rod
• Post VII: Special relativity and the rod/slot paradox – VII – no paradox for a collision scenario and consistency between all relevant LTs

Setup of a “transit scenario”

The reader may have got the impression that we have handled the “rod slot paradox” very one-sided. He or she may even ask whether we somehow removed the paradox by focusing on a “collision” and its special initial conditions. Should we not define another scenario, in which the rod can move through the slot? And does the “paradox” not result from a (seeming) equivalence of two such contradicting scenarios in certain frames of reference?

I agree completely with the suggestion to investigate a “transit scenario”. It is time to study a different setup of the rod/slot encounter – such that the rod can move through the slot. However, in the rod’s frame we would expect some length contraction of the slot, if the latter moves diagonally towards the rod (or vice versa). This makes the rod too long for the slot. This leads us directly to a rather simple question:

How can we move a long needle through a narrow slot in a metal plate, if the slot’s length is shorter than the needle’s length?

The very simple answer is that you just have to rotate the plate – or the needle. Such that the needle’s right end glides under the right edge of the slot and can then move diagonally with an appropriate horizontal velocity component (fitting the angle and the objects’ dimensions) through the slot.

Meaning: In a reference frame in which the slot is too short, we need an inclination angle between the rod and the slot. From the perspective of an observer who experiences the rod horizontally at rest, this might look like as depicted in the following drawing:

 

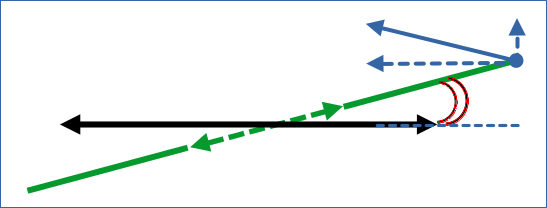
Illustration 1: Rod can move though the slot due to an inclination angle and fitting velocity components

The blue vector indicates a velocity of the slot upwards (in y-direction) and to the left (in negative x-direction). We understand that the horizontal and vertical velocity components must fit the inclination angle and the lengths of the slot and the rod to avoid a collision with the plate. A particular fine-tuning of velocity components and the inclination angle would be required if the transit of the slot started when the slot’s right end just passed the rod’s right end. The upward velocity component then must be limited such that the slot’s left end does not reach the y-level of the rod before the slot reaches the left end of the rod.

How to set up a “transit scenario”?

During the analysis of the collision scenario we saw that an inclination angle in the slot’s frame became apparent after the application of a Lorentz Transformation to the coordinates of the rod, which moved vertically in our setup-frame A. The target frame of the LT, frame B, instead co-moved horizontally with slot.

However, due to the downward motion of the rod the resulting inclination angle had a wrong orientation in comparison to what we need for a transit scenario. If you go back to the previous posts and look at the drawings there, you will find that the (smaller) angle between the slot and the rod was always positive (0 < Ψ_r < π/2), whilst the (smaller) angle between the slot and the relative velocity vector was negative (but > – π/2).

Now, we instead need a negative angle between the slot and the rod (0 > Ψ_r > – π/2) together with a negative angle between the slot and the relative velocity (> – π/2). But, if you try it out you will soon realize that we cannot get this by just mirroring the collision scenario set up in frame A across either of its coordinate axes or by rotating the scenario by multiples of π/2.

What we instead have to do is to switch the roles of the slot and the rod in our setup done in the 2nd post of this series. I.e. we move the slot upwards in y-direction (in a frame Z), only, and instead let the rod move horizontally. See illustration 2 below:

 

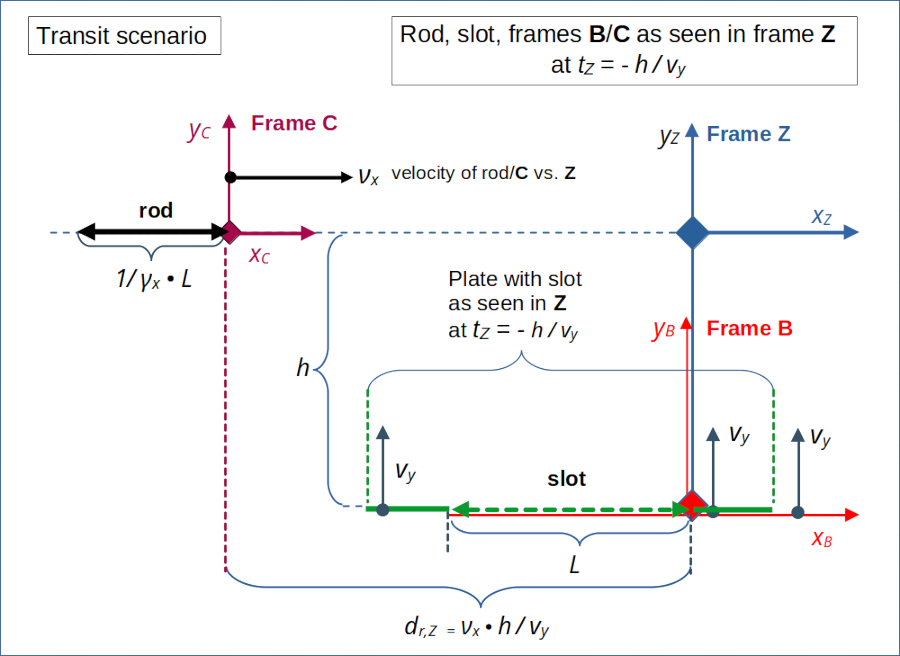
Illustration 2: Setup of the ” Transit Scenario” in a frame Z. In Z, the plate with the slot moves vertically upwards in y-direction, but does not move not in x-direction. Frame B is co-moving with the slot, while frame C is co-moving with the rod in horizontal x-direction at y_Z = 0.

I have renamed the setup frame to “Frame Z“, as it would move horizontally vs. our original frame A used for the collision scenario. The initial placements of the objects are such that the right end of the rod meets the right end of the slot at t_Z = 0. See illustration 3.

 

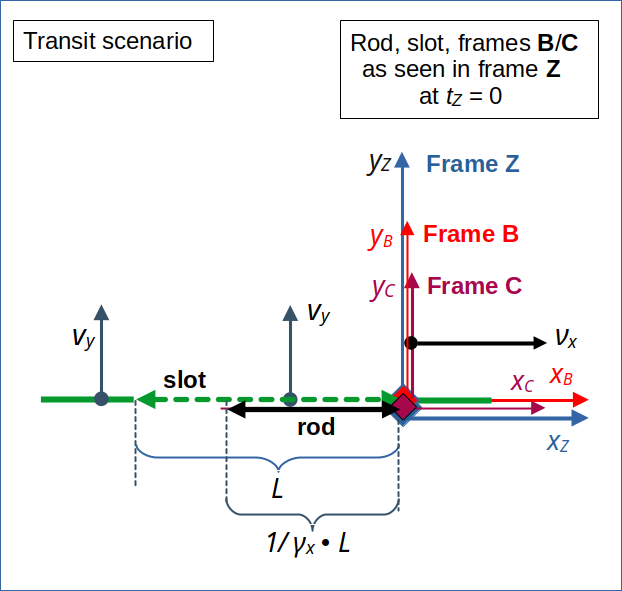
Illustration 3: “Transit Scenario” – the right end of the vertically moving slot meets the right end of the horizontally moving rod in a frame Z at t_Z = 0. As the rod, due to length contraction, is shorter than the slot, the slot just passes the rod without collision. This is, of course, an idealized extreme scenario for infinitesimally thin objects.

As for the collision scenario we have assumed that both rod and slot have the same proper length L and are oriented parallel to each other in Z. We have selected Cartesian coordinate systems B and C such that the orientations of the rod and the slot fit to the orientation of the x-axes. I.e. in frame C the rod stretches along the x_C-axis and in B the slot is oriented along the x_B-axis. Frame C and B have parallel x-axes in Z. Rod and slot have infinitesimal extensions in y- and z-direction.

Of course, our “transit scenario” is an extreme scenario, which only would work for infinitesimally thin objects in y-direction. We just look at last possible moment for a transit of the rod through the vertically moving slot.

You may also wonder why I ordered things such that the right ends of the rod and the slot reach x_Z = at time t_Z = 0. This setting makes some calculations in the forthcoming posts a bit simpler. The reader is free to change the timing (and subsequent calculations) such that the rod’s right end does not pass x_Z = 0, but x_Z = – ε [for some small ε) at t_Z = 0. It will not change the basic results we are going to derive.

Potential paradox ?

When we naively change perspectives and argue that an observer co-moving with the rod would see a length contraction of the slot, then we might argue the rod must collide with the diagonally upwards moving slot.

However, such a line of argumentation does not include an option for a potential rotation of the slot – due to relativistic effects in two dimensions. Our hope is that any potential paradox will disappear in the course of a proper application of the Lorentz Transformation between the observers co-mving with the the slot and re rod. As we found it for the even more confusing collision scenario.

Equivalence of the transit scenario and the collision scenario?

The switch of roles of our slot/rod objects appears to be somewhat strange on first sight – as from a fully Newtonian point of view the change in velocity vectors theoretically leads to a fully equivalent scenario. A rotation by – π/2 and afterwards a mirroring across the y-axis does not affect lengths in Newtonian physics and the size (norm) of velocity components.

However, length contraction and time dilation of SR affect the objects differently in frame Z in comparison to hat we experienced in A. We clearly have a situation in which, due to length contraction of the horizontally moving rod, a transit of the rod through the slot should be possible. But is this not just our “paradox”?

No, it is not. We have set up a different scenario in frame Z compared to the collision scenario in frame A. There is no Lorentz Transformation between frames A and Z which would transform the initial conditions assumed for the collision scenario in A to the conditions defined in Z above. We will<explicitly show this is a future post. Thus, we would get a “paradox”, only, if we found a collision for the our transit setup by one of the observers in the frames Z, B and C. We shall prove that this is not the case.

Readers who have followed all the arguments for the collision scenario and the transformation to the slot’s frame B, already see that we, indeed, have defined a different scenario in frame B. The angle between the rod and the slot is bound to become Ψ_r = 0 during a LT from frame Z to frame B. This is a special value for Ψ_r to allow for an unhindered passage of the rod. Thus in frame B the elementary difference between the scenarios becomes obvious. Something analogous holds for frame C.

We must start to accept that the inclination angle between the slot and the rod in the slot’s frame actually is a free parameter of the initial conditions, and that it is a property affected by the LT. Our two scenarios mark the ends of a wider spectrum of scenarios.

Remark for the experienced physicists: The order of rotations and mirror processes matters, and boosts along different axes have different effects. Boosts in SR along different axes do not commute, either. It is not the same whether we first boost for a horizontal motion and then for a vertical one or vice versa. This is one of multiple reasons why the setup of the transit scenario is profoundly different from the setup of the collision scenario – at least in the context of SR.

Conclusion

In this post we have set up a scenario in which the rod should pass the slot without a collision. We hope that applying the Lorentz Transformation between the reference frames of different observers will again show us that Einstein#s Special Theory of Relativity avoids any potential paradoxes due to a proper relativistic rotation of the slot vs. the rod and a resulting inclination angle. The combination should support a collision-free transit of the rod through the slot in critical inertial frames where an observer measures a length-contracted slot. We also want to show that the transit scenario is profoundly different from the collision scenario regarding its initial conditions – and that this fact removes other potential contradictions.

See the next post

Special relativity and the rod/slot paradox – IX – transit scenario and measurements by an observer co-moving with the rod

for the transformation of the coordinates of key events during the transit from frame Z to frame C co-moving with the rod.