After a new web location exists for anracon some of my friends might be interested in what I do in my free time as a retired man. Regarding IT I privately work with 3 topics in very different fields:

• Virtual VLANs, Linux namespaces, veth, Linux Bridges, routes, ARP, packet filtering
• Organization of the latent space of Autoencoders based on Deep CNNs and ResNets
• The mathematics of multivariate normal distributions

All of these topics are not really new. The first topic had its origin in 2016 when I had to reorganize the virtualization in my own small company. The second came up by accident during the preparation of a series of seminar talks for my employer at that time. The third stems from spring 2023 when I found some time to dive into some math stuff again I once had learned at University.

Some information why I think these topics are interesting – even for a retired person and on the level of a hobby:

Virtual VLANs, Linux namespaces, veths, Linux bridges, security

As a Linux enthusiast I still organize some of my private servers and test systems as KVM guests and LXC containers on a virtualization host. In 2016 and 2017 I got interested in how one can control and isolate the traffic between such systems via virtualized VLANs. This lead to an unfinished post series in my Linux Blog.

In March 2024 a nice American guy working with Cisco products contacted me. He was interested in specific questions regarding the impact of routes in namespace setups with veth connections and ARP-traffic between namespaces or virtualized hosts along VLANs. The very fruitful discussion made me pick up the whole topic again in much deeper detail.

Most of these details are in my opinion relevant with respect to security. The results of new experiments will be discussed in a new post series in my Linux Blog.

Machine Learning: Latent space organization by deep generative Autoencoders

I followed Machine Learning privately from 2015 onwards when I had found out that a kind of Supply Chain network can be mapped to graphs dealt with in deep neural networks. In the last decade there was a lot of discussion about the organization of data in the so called latent space of generative Autoencoders and Variational Autoencoders. While we have much more advanced ML-tools these days, the topic is still fascinating. Reason: It casts some light on the question of how a neural network structures information gather during training about object features in a latent vector space.

For images with human faces I found that a standard CNN-based Autoencoder organized the data in form of an off-center multivariate normal distribution [MVD] with ellipsoids as hyper-surfaces of constant probability density.

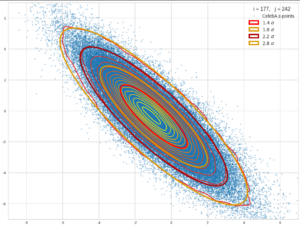
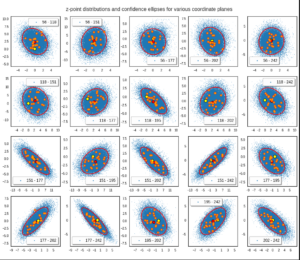
In this sense enforcing a distribution close to a normal one via the Kullback-Leibler [KL] divergence term added to the loss appeared to be superfluous. As soon as we can determine the location and the primary axes of the MVD we can also deal with feature arithmetic in the latent space.

I have shown that the multidimensional ellipsoidal data distribution in the latent space with 200 to 500 dimensions only covers a very small volume. But data points this volume (and respective vectors) can indeed be used to generate new and relatively sharp face images by statistical methods. Sharper than the images shown in some introductory books under comparable network conditions. I have written about this topic already in my Linux Blog. However, I want to use as a first major post series in my coming blog on Machine Learning experiments.

An interesting question is whether the MVD data distribution depends not only on typical face features which may follow natural Gaussian distributions, but also on specific properties of a standard sequence of a few (4 to 5) Convolutional Neural Layers. To analyze this a bit better I want to write a ResNet based Autoencoder with a much higher depth of Convolutional layers (110 to 164). I expect better images, but again a high-dimensional MVD.

Afterward, I want to look at other test data very different from human faces. An interesting question is, how the latent space is filled if and when we offer the Neural Network a latent space with more dimensions than basic features. Will we also get some kind of compact,well structured distribution for the probability density in the latent space? Without enforcing an artificial compactification via KL-loss terms? One should not forget that Variational Autoencoders are often used, because a very low dimensional latent space is filled in a strange way when the network is forced to use it. Things may change substantially with a higher number of latent space dimensions …

Mathematics of Multivariate Statistical Distributions

A combination of Multidimensional Analysis, Linear Algebra and (Geometrical) Projections on hyper-planes governs statistical Multivariate Normal Distributions in high dimensional vectorspaces. This is a fascinating topic in itself. And it has some overlap with the topic of Primary Component Analysis of data in Machine Learning, not only in the original feature space of the data, but also in latent vector spaces after training.

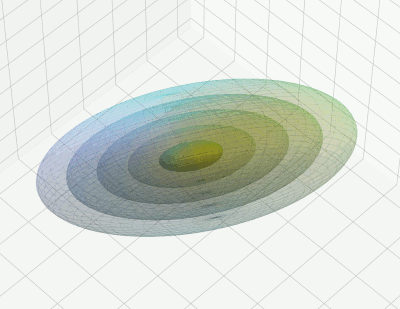
I think that due to the fact that such distributions appear in some areas of Machine Learning one should cover the basic math to some extent for interested readers. With practical applications in the analysis of ML date in latent spaces. I have all the required math stuff ready, but have not found the time to write it up in a concise way.

So, that is what I use some of my free time for these days. If someone of my friends is interested in one of these topics, he/she is invited to participate.