Special relativity and the rod/slot paradox – XV – velocities of colliding rod and slot in a diagonally moving frame

In the preceding two posts we have derived x– and y-coordinates of the rod’s and the slot’s ends in a new frame W. W‘s origin moves in a diagonal direction vs. the origin of our setup frame A, which we used to define the collision scenario (see previous posts, in particular the 12th post of this series). In W both the rod and the slot are perceived as being rotated vs. the line of relative motion between W and A. The rotation angles are different.

In this post we shall derive and analyze the velocities of the rod and slot in W. We will use the results in yet another post to predict an inevitable collision in W, too.

Previous posts:

Lorentz Transformation of velocity components between A and W

The rotated coordinate systems used in the last 4 posts had an x-axis (x_rel,A) aligned with the line of relative motion of W vs. A. In A the x-coordinate axis points into the direction of W. However, W approaches A in negative x_rel,A – direction. The absolute value of the relative velocity between W and A is just v_rel.

Rotated coordinate systems of frames A and W

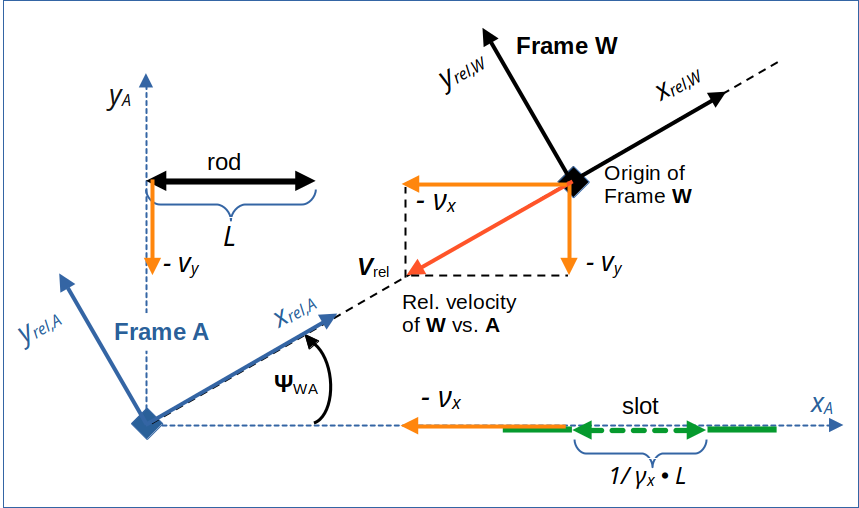
Illustration 1: A diagonally approaching frame W in our collision scenario, which was set up in a frame A. For the Lorentz Transformation from A to W we use rotated Cartesian coordinate systems with x-axes oriented along the line of relative motion of the frames.

I first want to remind you of some formulas regarding the transformation of velocity components of objects moving in reference frame A to respective components in the approaching frame W. We just have to adapt the formulas given in the 3rd post of this series. We name the component of the velocity of an object O in A parallel to the line between the origins of W and A v_o,x,rel,A. The perpendicular component gets the name v_o,y,rel,A. Then we have

\[ \begin{align} v_{o,x,rel,W} \,&=\, { \, v_{o,x,rel,A} + v_{rel} \, \over 1 + v_{o,x,rel,A} * v_{rel} / c^2} \, &\quad v_{o,x,rel,A} \,&=\, { \,v_{o,x,rel,W} \,-\, v_{rel} \, \over 1 \,-\, v_{o,x,rel,A} * v_{rel} / c^2} \\[10pt] v_{o,y,rel,W} \,&=\, { \,v_{o,y,rel,A} * \sqrt{\,1 \,-\, \beta_{rel}^2 \, } \over 1 + v_{o,x,rel,A} * v_{rel} / c^2} \, &\quad v_{o,y,rel,A} \,&=\, { \,v_{o,y,rel,W} * \sqrt{\,1 \,-\, \beta_{rel}^2 \, } \over 1 \,-\, v_{o,x,rel,W} * v_{rel} / c^2} \end{align} \]

The relativistic factors related to v_rel are

\[ \begin{align} v_{rel}^2 \,&=\, v_{rel,w2a}^2 \,=\, \nu_x^2 \,+\, v_y^2 \,, \\[8pt] \beta_{rel}^2 \,&=\, \beta_{w2a}^2 \,=\, { 1 \over c^2}\, \left(\, \nu_x^2 \,+\, v_y^2 \,\right) \, =\, \beta_x^2 \,+\, \beta_y^2 \,, \\[8pt] \gamma_{rel}^2 \,&=\, \gamma_{w2a}^2 \,=\, {1 \over 1 \,-\ \beta_{rel}^2 } \,=\, {1 \over 1 \,-\ \beta_x^2 \,-\, \beta_y^2} \,. \end{align} \]

Transformation of the slot’s velocity components to frame W

We use some results of the preceding posts and hop over details of the derivation. We first have to find the components of the slot‘s velocity vector v_s,A along the line connecting the origins of A and W. This line has an inclination angle Ψ_WA relative to the standard coordinate axis x_A. We call the component parallel to the rotated axis x_rel,A in A (aligned with the line) v_s,x,rel,A. The component along the perpendicular axis y_rel,A is named v_s,y,rel,A. We calculate them to be

\[ \begin{align} v_{s,x,rel,A} \,&=\, – \nu_x * \cos\left(|\Psi_{WA}|\right) \,=\, – \, \nu_x * {\beta_x \over \beta_{rel}} \,, \\[8pt] v_{s,y,rel,A} \,&=\, + \nu_x * \sin\left(|\Psi_{WA}|\right) \,=\, + \, \nu_x * {\beta_y \over \beta_{rel}} \,. \end{align}\]

Thus

\[ \begin{align} v_{s,x,rel,W} \,&=\, {v_{rel} \,-\, \nu_x * \left(\beta_x / \beta_{rel} \right) \over 1 \,-\, \nu_x \, \left(\beta_x / \beta_{rel} \right) \, \left( v_{rel} / c^2 \right) } \,, \\[8pt] v_{s,y,rel,W} \,&=\, + {1 \over \gamma_{rel}}\, {\nu_x * {\beta_y / \beta_{rel}} \over 1 \,-\, \nu_x \, \left(\beta_x / \beta_{rel} \right) \, \left( v_{rel} / c^2 \right) } \,. \end{align}\]

The denominator is equivalent to

\[ 1 \,-\, \nu_x \, \left(\beta_x / \beta_{rel} \right) \, \left( v_{rel} / c^2 \right) \,=\, {1 \over \gamma_x^2} \,. \]

We conclude

\[ \begin{align} v_{s,x,rel,W} \,&=\, + \, \gamma_x^2 * \nu_x * \left(\beta_x / \beta_{rel} \right) *c \,, \\[8pt] v_{s,y,rel,W} \,&=\, + \, \gamma_x^2 * {1 \over \gamma_{rel}} \, {\beta_x \, \beta_y \over \beta_{rel}} * c \,. \end{align}\]

After some intermediate steps we get for the absolute value of the slot’s velocity v_s,W in W

\[ v_{s,W} \,=\, \gamma_x \, \beta_y * c\,,\quad \beta_{s,W} = \gamma_x\, \beta_y \,. \]

The angle Ψ_sv,rel,W of the velocity vector with respect to the line of relative motion (of W vs. A) is given by

\[ \begin{align} \cos \left( \Psi_{sv,rel,W} \right) \,&=\, { v_{s,x,rel,W} \over v_{s,W}} \,=\, \gamma_x\,{\beta_y \over \beta_{rel}} \,, \\[8pt] \sin \left( \Psi_{sv,rel,W} \right) \,&=\, { v_{s,y,rel,W} \over v_{s,W}} \,=\, {\gamma_x \over \gamma_{rel} } \,{\beta_x \over \beta_{rel} } \,. \end{align} \]

We compare this to the angle of the slot with the line connecting the origins of frames A and W (see previous posts)

\[ \begin{align} \cos \left( \Psi_{s,rel,W} \right) \,&=\, {\gamma_x \over \gamma_{rel} } \,{\beta_x \over \beta_{rel}} \,, \\[8pt] \sin \left( \Psi_{s,rel,W} \right) \,&=\, – \gamma_x\,{\beta_y \over \beta_{rel}} \end{align} \]

to derive

\[ \begin{align} \cos \left( \Psi_{sv,rel,W} – \Psi_{s,rel,W} \right) \,&=\, 0 \, \quad \Rightarrow \\[8pt] \Psi_{sv,rel,W} – \Psi_{s,rel,W} \,&=\, \pi / 2\,. \end{align} \]

This also follows from the sine values. Meaning:

The velocity vector of the slot in W is perpendicular to the slot itself there.

See illustration 2 at the end of this post.

Transformation of the rod’s velocity components to frame W

The velocity components of the rod in A parallel and vertical to the line of the frames’ relative motion are:

\[ \begin{align} v_{r,x,rel,A} \,&=\, – v_y \, {\beta_y \over \beta_{rel}} \,, \\[8pt] v_{r,y,rel,A} \,&=\, – v_y \, {\beta_x \over \beta_{rel}} \,. \end{align}\]

Consider the negative signs! The LT tells us

\[ \begin{align} v_{r,x,rel,W} \,&=\, {v_{rel} \,-\, v_y * \left(\beta_y / \beta_{rel} \right) \over 1 \,-\, v_y \, \left(\beta_y / \beta_{rel} \right) \, \left( v_{rel} / c^2 \right) } \,, \\[8pt] v_{r,y,rel,W} \,&=\, – {1 \over \gamma_{rel}}\, {v_y * {\beta_x / \beta_{rel}} \over 1 \,-\, v_y \, \left(\beta_y / \beta_{rel} \right) \, \left( v_{rel} / c^2 \right) } \,. \end{align}\]

The denominator has the following value:

\[ 1 \,-\, v_y \, \left(\beta_y / \beta_{rel} \right) \, \left( v_{rel} / c^2 \right) \,=\, {1 \over \gamma_y^2} \,. \]

Using this gives

\[ \begin{align} v_{r,x,rel,W} \,&=\, + \, \gamma_y^2 * \left(\beta_x^2 / \beta_{rel} \right) *c \,, \\[8pt] v_{r,y,rel,W} \,&=\, – \, {\gamma_y^2 \over \gamma_{rel}} \, {\beta_x \, \beta_y \over \beta_{rel}} * c \,. \end{align}\]

For the absolute value of the rod’s velocity v_r,W in W we get (after some steps)

\[ v_{r,W} \,=\, \gamma_y \, \beta_x* c\,,\quad \beta_{s,W} = \gamma_y\, \beta_x \,. \]

The angle Ψ_rv,rel,W of the rod’s velocity vector with respect to the line of relative motion (of W vs. A) is given by

\[ \begin{align} \cos \left( \Psi_{rv,rel,W} \right) \,&=\, \gamma_y\,{\beta_x\over \beta_{rel}} \,, \\[8pt] \sin \left( \Psi_{rv,rel,W} \right) \,&=\, -\, {\gamma_y \over \gamma_{rel} } \,{\beta_y \over \beta_{rel} } \,. \end{align} \]

We compare this to the angle of the rod with the line connecting the origins of frames A and W (see preceding posts)

\[ \begin{align} \cos \left( \Psi_{r,rel,W} \right) \,&=\, \gamma_y \,{\beta_x \over \beta_{rel}} \,, \\[8pt] \sin \left( \Psi_{r,rel,W} \right) \,&=\, – {\gamma_y \over \gamma_{rel}} \,{\beta_y \over \beta_{rel}} \,. \end{align} \]

Meaning:

The velocity vector of the rod in W is aligned with the rod itself there.

See illustration 2 below.

Schematic sketch of the perceived situation

The situation in W at t_W = 0 is depicted below.

Collision scenario and velocities in frame W

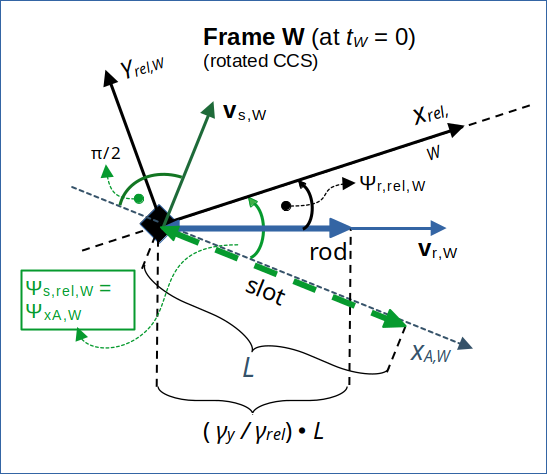
Illustration 2: Collision scenario seen from a diagonally approaching frame W. The scenario was set up in a frame A (see the first posts of this series). For the Lorentz Transformations from A to W we use rotated Cartesian coordinate systems with their x-axes oriented along the line of relative motion of the frames. The velocity of the slot is oriented perpendicular to the slot. The velocity of the rod is aligned with the rod’s orientation.

There are good reasons why the velocities vectors must be oriented in W the way which we have derived above. We will come back to this point in a future post.

Conclusion

We have investigated how the velocities of the rod and the slot are perceived in a frame W, which approaches the setup frame A on a diagonal path. We found that the slot’s velocity is perpendicular to the slot’s orientation in W. The rod’s velocity transports the rod aligned with its orientation. These were interesting findings by themselves.

However, we still have to show that the situation perceived in W at t_W = 0 leads to an unavoidable collision between the rod and the slot. This is the topic of the next post in this series.

Stay tuned ….